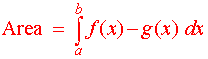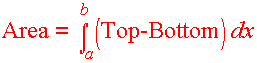Area Between Two Curves

Recall that the area under a curve and above the x-axis can be computed by the definite integral.  If we have two curves

        y  =  f(x)     and     y  =  g(x)

such that 

        f(x)  >  g(x) 

then the area between them bounded by the horizontal lines x  =  a and x  =  b is

To remember this formula we write

Example 

 Find the area between the curves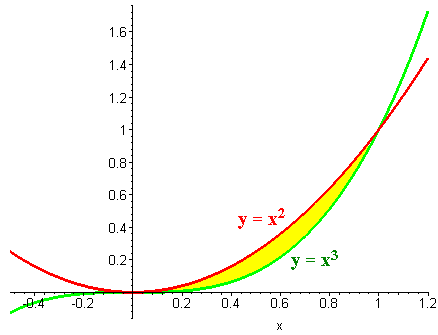 

        y  =  x²  

and 

        y  =  x³ 

Solution

First we note that the curves intersect at the points (0,0) and (1,1).  Then we see that

        x³  < x²  

in this interval.  Hence the area is given by

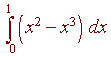
         = 1/3 - 1/4 = 1/12.

Exercises

1. Find the area between the curves y = x² and y =         
   
   

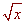
2. Find the area between the curves y = x² - 4 and y = -3x       
   
   

3. Find the area between the curves y = 2/x  and y = -x + 3       
   
   

4. Find the area between the curves y =  3^x   and y = 2x + 1       

Application

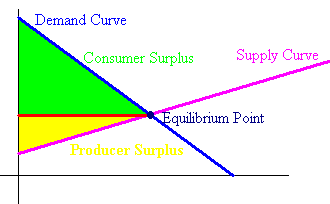
Let y = f(x) be the demand function for a product and y = g(x) be the supply function.  Then we define the equilibrium point to be the intersection of the two curves.  The consumer surplus is defined by the area above the equilibrium value and below the demand curve, while the producer surplus is defined by the area below the equilibrium value and above the supply curve.  

Example  

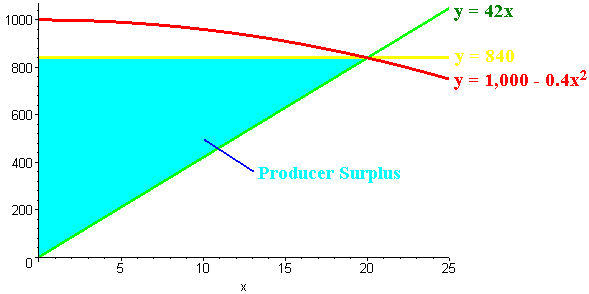
Find the producer surplus for the demand curve

        f(x) = 1,000 - 0.4x²  

and the supply curve of 

        g(x) = 42x

Solution

We first find the equilibrium point:

We set 

        1,000 - 0.4x² = 42x

or 

        0.4x² + 42x - 1,000 = 0

We get 

        x = 20 

hence

        y = 42(20) = 840

We integrate

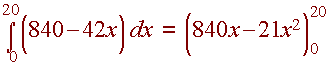
        = 8400 

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions