Limits

Example

Consider the function 

                           x² - 1
        f(x) =                                
                        x² +2x - 3

If we plug in 1 we arrive at 0/0 which is undefined.  What does this function look like near x = 1?

We can construct the following table:

x	.9	.99	1.1	1.01	1.001
f(x)	.487	.499	.512	.501	.5001

We can see that this function approaches .5 as x approaches 1.  Below is the graph of this functions.

This example leads us to the following definition

 

Definition of the Limit If f(x) becomes arbitrarily close to a single number L as x approaches c form either side then

We can think of the definition of a limit as x -> c as two hikers, one traveling from the right and the other traveling from the left.  If they will hike towards the same place, then that place is called the limit.  

Properties of Limits

suppose that 

and that a is a constant.  then

A)  

B)  

C)  

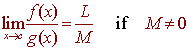
D) 

 E) 

Example

Suppose that 

then 

Algebra and Limits

When finding a limit, always plug in the number first.  If you get a defined value, then that is the answer.  Otherwise you may have to do algebra to find the limit.

Example:

lim as x -> 1 (x² - 1)/(x² +2x - 3)

= lim as x -> 1  (x - 1)(x + 1)/(x + 3)(x - 1)

= lim as x -> 1 (x + 1)/(x + 3) = 2/4 = .5

Find the limit

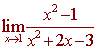
Solution

Notice first, if we plug in 1 for x, we get 0/0.  The algebra that will work is factoring.

Now plug in 1 to get

        2/4  =  1/2

Example

Find the limit

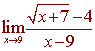
Solution

Again, if we plug in, we get 0/0.  What kind of algebra will work for this problem?  Recall from basic algebra how to rationalize the denominator.  Our strategy, will be to rationalize the numerator.  We multiply the numerator and the denominator by the conjugate root.

Now we can plug in 9 for x to get

            1              1
                     =          
        4 + 4            8

One Sided Limits

We define the left limit

as the y coordinate of the curve as the point moves from the left.

Similarly, we define the right limit  

as the y coordinate of the curve as the point moves from the left.

Example

Find

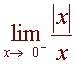
Solution

The graph of the function is pictured below.

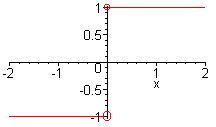
Taking a stroll from the left hand side, the y value approaches -1.  Hence the limit is -1.  Notice that without the "-" sign, the limit would not exist.

We say that the limit exists if the left and the right limits are equal.

Unbounded limits

Example

Find

Solution

Plugging in 2 we get 6/0 which is undefined.  If we plug in a number to the left of 2, such as 1.99999, we get a very large negative number.  We say that the limit is negative infinity.

Back to the calculus home page

Back to the math department home page

e-mail Questions and Suggestions