Increasing and Decreasing Functions
Definition of Increasing and Decreasing
We all know that if something is increasing then it is going up and if it is decreasing it is going down. Another way of saying that a graph is going up is that its slope is positive. If the graph is going down, then the slope will be negative. Since slope and derivative are synonymous, we can relate increasing and decreasing with the derivative of a function. First a formal definition.
|
Definition of Increasing and Decreasing A function is increasing on an interval if for any x1 and x2 in the interval then x1 < x2 implies f(x1) < f(x2) A function is decreasing on an interval if for any x1 and x2 in the interval then x1 < x2 implies f(x1) > f(x2) |
How does this relate to derivatives? Recall that the derivative is the limit
f(x2) - f(x1)
x2 - x1
If x1 < x2, then the denominator will be positive. If also f(x1) < f(x2), then the numerator will be positive, hence the derivative will be positive. On the other hand if f(x1) > f(x2), then the numerator will be negative and the derivative will be negative. this leads us to the following theorem.
|
Theorem on Derivatives and Increasing/Decreasing Functions Let f be a differentiable function on the interval (a,b) then
|
Examples and Critical Numbers
Example
Determine the values of x where the function
f(x) = 2x3 + 3x2 - 12x + 7
Solution
We first take the derivative
f '(x) = 6x2 + 6x - 12
To determine where the derivative is positive and where it is negative, find the roots. Factor to get
6(x2 + x - 2) = 6(x - 1)(x + 2)
Hence the change in sign can occur when
x = 1 and x = -2
Now create some test values
| x | f '(x) |
| -3 | 24 |
| 0 | -12 |
| 2 | 24 |
The derivative is positive outside of [-2,1] and is negative inside of [-2,1]. We can conclude that f is increasing outside of [-2,1] and decreasing inside of [-2,1]. The graph is shown below.
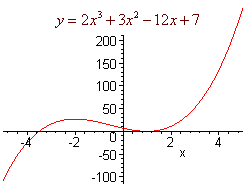
We saw that the values of x such that the derivative is 0 was of special interest. Other points where there could be a change from increasing to decreasing is where the derivative is undefined.
We call c a critical number if either f '(c) = 0 or f '(c) is undefined.
Example
Determine where the function below is increasing and where it is decreasing.
2
f(x)
=
+ 18x
x - 1
2
f(x)
=
+ 18x
x - 1
Solution
Since f(x) is not continuous at x = 1, it is also not differentiable there. Hence x = 1 is a critical point. To find other critical points, we take a derivative. It is helpful to use negative exponents instead of fractions here.
f '(x) = [2(x - 1) -1 + 18x]' = -2(x - 1) -2 + 18 = 0
18 = 2(x - 1) -2 Divide by 2 and multiplying by (x - 1)2
9(x - 1)2 = 1 Take the square root of both sides
3(x - 1) = 1 or 3(x - 1) = -1
x = 4/3 or x = 2/3
This gives us three critical points
x = 2/3 x = 1 and x = 4/3
Now construct a table and determine positive intervals and negative intervals
-2(x - 1) -2 + 18
| x | f '(x) |
| 0 | Positive |
| .9 | Negative |
| 1.1 | Negative |
| 2 | Positive |
We can conclude that f is increasing for values of x less than 2/3 and values of x greater then 4/3. f is decreasing for values between 2/3 and 4/3 excluding x = 1. A graph of f is shown below.
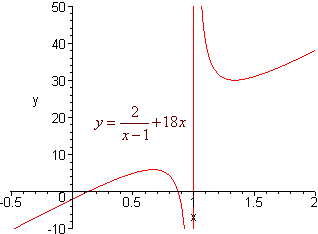
Application
The weight (in pounds of a newborn infant during its first three months of life can be modeled by
W = 1/3 t3 + 5/2 t2 - 19/6 t + 8
where t is measured in months. Determine when the infant was gaining weight and when it was losing weight.
Solution
We are asked to find when the function is increasing and when it is decreasing. We have
W' = t2 + 5t - 19/6
Using the quadratic formula or a calculator we get
0.56 or -5.56
Since the domain is stated to be between 0 and 3, we use only 0.56. Now construct a table
| t | W'(t) |
| 0 | Negative |
| 1 | Positive |
Hence the function is increasing for t greater than 0.56 and decreasing for t smaller than 0.56
We can conclude that the infant was losing weight for the first 0.56 months of its life and then began gaining weight afterwards at least up to the third month.
Back to the calculus home page
Back to the math department home page
e-mail Questions and Suggestions