Asymptotes

Horizontal Asymptotes

We define a horizontal asymptote of a function as the limit as x approaches infinity (or negative infinity).  Symbolically, we write

 

Definition of a Horizontal Asymptote If            then we say that L is a horizontal asymptote of f(x).

We can also take the limit as x approaches negative infinity and also call the result a horizontal asymptote of f(x).  For rational functions the limits are always the same.  On the other hand absolute value and root functions can have two different horizontal asymptotes.

Example

Find the horizontal asymptote of

Solution

We divide numerator and denominator by the highest power of x (x²).  

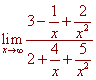
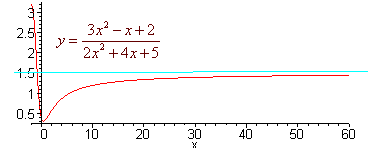
Now when we plug in, we get 3/2.  That is 3/2 is a horizontal assymptote.  The graph is shown below.

Exercises

Find the horizontal asymptotes of the following.  Hold your mouse on the yellow rectangle for the answer.

A.                      3x³ - 5x + 1
             y  =                                      
                         6x³ + 3x² - 4

B.                       7x² - 3x + 2
             y  =                                      
                         5x³ - 4x² + 10

Example

Find the horizontal asymptote of 

Solution

We find the limit

by dividing numerator and denominator by x.

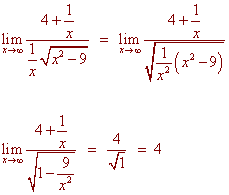
We are not done, since when we encounter an irrational function, we must check the left horizontal asymptote.  We next take the limit as x approaches negative infinity.  Again we divide both numerator and denominator by x.  We get

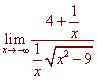
We can not bring the 1/x into the square root sign since it is negative.  For x negative,

Substituting gives

        We can conclude that the function has a left horizontal asymptote of -4 and a right horizontal asymptote of 4.  The graph is shown below.

Vertical Asymptotes

A reduced rational function  will have a vertical asymptote when the denominator is 0.  Once we know that a function has a vertical asymptote at x  =  c, we then need to find the limit as x approaches c form the left and from the right.  The limit will always be infinity or negative infinity, so we only need to check for the sign of the limit.

Example:

Describe the vertical asymptote of

                     1
        y =                   
                   x - 1

Solution

We see that when x = 1, the function will have a vertical asymptote. note that to the left of 1 (plug in 0.9) the function is negative and to the right of 1 (plug in 1.1) the function is positive, hence

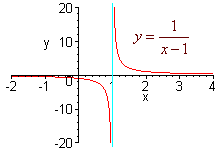
Application

Example:  

If a person jumps from an airplane, his velocity is modeled by

                         -32t
        v(t) =                      
                     0.01t + 1

What is his terminal velocity?

Solution

Terminal velocity means the velocity after an infinite amount of time.  

We find

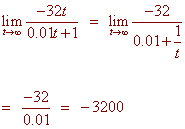
The terminal velocity of the jumper is 3200 feet per second downward.

Example

The population P after t years of a newly introduced species of wildcat can be modeled by the equation

What is the equilibrium population (the population at time approaches infinity)?

Back to the calculus home page

Back to the math department home page

e-mail Questions and Suggestions