The Gradient

I.  Quiz

II.  Homework

III.  Directional Derivatives

Suppose you are given a topo map and want to see how steep it is from a point that is neither due West or due North.  Recall that the slopes due north and due west are the two partial derivatives.  The slopes in other directions will be called the directional derivatives.  Formally, we define

Definition  Let f(x,y) be a differentiable function and let u be a unit vector then

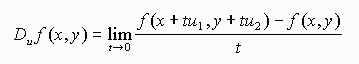
Notice that if u is i then the directional derivative is just delf/delx and if u is j the it is delf/dely.

Theorem:

Let f(x,y) be a differentiable function, and u be a unit vector with direction theta, then

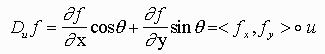
Example:  Let f(x,y) = 2x + 3y² - xy and v = <3,2> Find D_v f(x,y)

We have delf/delx = 2 - x and delf/dely = 6y - x, and ||v|| = sqrt(9 + 4) = sqrt(13)

Hence

D_v f(x,y) = <2 - y,6y - x>@<3/sqrt(13),2/sqrt(13)> = 2/sqrt(13) (2 - y)  + 3/sqrt(13) (6y - x)

Exercise

Let f(x,y) = e^xy2 and v = <2,-5>

Find  D_v f(x,y)

IV.  The Gradient

We define grad f = <f_x,f_y>

Notice that  

D_u f(x,y) = grad f @u

Theorem

1)  If grad f(x,y) = 0 then for all u, D_u f(x,y)

2)  grad f(x,y) is the maximal directional derivative direction.

3)  grad f(x,y) is the minimal directional derivative direction.

Proof:  

1)  If grad(x,y) = 0 then   D_u f(x,y) = grad f @u = 0@u = 0

2) and 3)  D_u f(x,y) = grad f @u  = ||grad f|| cos theta

This is a maximum when theta is 0 and a minimum when theta = pi.

If theta is 0 then grad f and u point in the same direction.  If theta = pi then u and grad f point in opposite directions.

Exercise:   Suppose that a hill has altitude w(x,y) = x² - y

Find the direction that is the steepest uphill and the steepest downhill.

V.  The Gradient and Level Curves

If f is differentiable at (a,b) and grad f not 0 at (a,b) then grad f is perpendicular to the level curve through (a,b).

We will show this geometrically.