Functions of Several Variables
I. Return Midterm II
II. Definition of Functions of Several Variables
A function of several variables is a function where the domain is a subset of Rn and range is R.
Example:
f(x,y) = x - y is a function of two variables
g(x,y,z) = (x - y)/(y - z)
is a function of three variables.
III. Finding the Domain
To find the domain of a function of several variables, we look for zero denominators and negatives under square roots:
Example
Find the domain of f(x,y) = sqrt(x - y)/(x + y)
The first we have x - y > 0
second we have x + y not= 0 hence we need to stay off the line y = -x
The domain is {(x,y)| x - y > 0 and y not= -x}
Exercise
Find the domain of the function f(x,y,z) = xyz/sqrt(4 - x2 - y2 - z2)
IV. Cylinders
Let C be a curve, then we define a cylinder to be the set of all lines through C and perpendicular to the plane that C lies in. We will explore cylinders using Math View.
V. Quadric Surfaces
Recall that the quadrics or conics are lines , hyperbolas, parabolas, circles, and ellipses. In three dimensions, we can combine any two of these and make a quadric surface. For example
z = x2 + y2
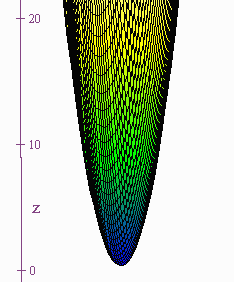
is a paraboloid since for constant z we get a circle and for constant x or y we get a parabola. We use the suffix -oid to mean ellipse or circle. We have:
x2/a2 + y2/b2 + z2/c2 = 1 is an ellipsiod
-x2/a2 - y2/b2 + z2/c2 = 1 is a hyperboloid of 2 sheets while
x2/a2 + y2/b2 - z2/c2 = 1 is a hyperboloid of 1 sheet
VI. Surface of Revolution
To let y = f(x) be a curve, then the equation of the surface of revolution abut the x-axis is
y2 + z2 = f(x)2