The Chain Rule

I.  Quiz

II.  Homework

III.  Review Of The Chain Rule For One Variable

Recall that if y = f(x) and x = x(t) then

dy/dt = dy/dx dx/dt

Suppose that y = f(x,y) = x² + 2x - xy + y²   and x(t) = t² +1, y(t) = t³ - t²  

Then what is dy/dt for t = 2

Solution:   f can be written as

(x(t))² + 2(x(t)) - x(t)y(t) + (y(t))²  

Hence the derivative is

2x(t)(x'(t)) + 2x'(t) - (x(t)y'(t) + y(t)x'(t)) + 2y(t)y'(t)   etc.

Instead we use the chain rule:

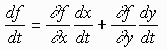
= (2x + 2 - y)(2t) + (-x + 2y)(3t² - 2t)

When t = 2, x(2) = 5 and y(2) = 8 - 4 = 4 hence

df/dt = 2(5 + 2 - 4)((2)(2) + (-5 + 2(4))(3(4) - 2(2)) = 48

Exercise:

Let f(x,y) = 2x -3xy and x(theta) = 2cos theta and y(theta) = 2sin(theta)

Find df/dtheta

IV.  The Chain Rule for 2 Variables

Let f(x,y) be a 2 variable function and x = x(u,v) and y = y(u,v) then

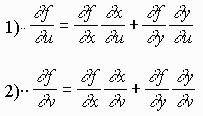
Example: Polar Coordinates

Let f(x,y) = x²y and x = rcos(theta) and y = rsin(theta)

then

delf/delr = delf/delx delx/delr + delf/dely dely/delr = 2xycos(theta + x²sin theta)

= 2r²cos²(theta)sin(theta) + r²cos²(theta)sin(theta) = 3r²cos²(theta)sin(theta)

Exercise  

Let f(x,y = x - 2y²  and x(u,v) = u - 2v, y(u,v) = 2u + v

find delf/delu and delf/delv

V.  Implicit Differentiation

Suppose we have the ellipsoid

x² + y²  + 2z² = 1

and we want to find delz/delx and delz/dely

We write

f(x,y,z) = f(x,y,z(x,y)) = 0

but 0 = delf/delx = delf/delx delx/delx + delf/dely dely/delx + delf/delz delz/delx

Where the first factors correspond to the partials with respect to the first, second and third variables respectively and the second factors are with respect to the actual x.

We have delx/delx = 1 and dely/delx = 0

Hence 0 = delf/delx + delf/delz delz/delx

So that

delz/delx = -delf/delx / delf/delz = -f_x/f_z

for the ellipsoid:

delf/delx = 2x/4z = x/2z