Polar Area and Acrlength

I.  Quiz

II.  Homework

III.  Area

If we have a region defined by r = r(theta), theta = a and theta = b, what is the area of the region?  

If r is the arc of a circle then we want to find the area of the sector of the circle.  If theta = b - a then the area = 1/2 theta r²

This is true since the area of the entire circle is pi r².  We can set up the relationship:

A/(pi r²) = theta/2pi so that A = (pi r² theta)/2pi = 1/2 theta r²

Cutting the region into tiny d theta pieces, we have

dA = 1/2 r(theta)² d theta

Adding up all the pieces, we arrive at

Exercise

Find the area enclosed by the curve r = 2cos theta

IV.  Arclength

Since the arclength of a parameterized curve is given by

int sqrt[(dx/dtheta)² + (dy/d theta)² ]d theta,

we have

that for polar coordinates, letting x(theta) = r(theta)cos(theta) = rcos(theta)

and y(theta) = r(theta)sin(theta) = rsin(theta)

we have

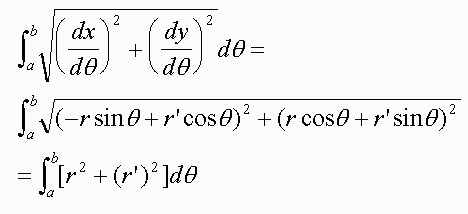
We also have that the surface area of revolution is

2pi int rsin(theta sqrt[r² + r'²]dtheta

Find the length of the 8 petalled flower r = cos(4 theta)

Solution:

We find the length of one of the petals and multiply by 8.

We see that the right petal goes through the origin at -pi/8 and next at pi/8.

Hence we integrate

int from -pi/8 to pi/8 sqrt(cos²(4 theta) + 18sin² (4 theta) d theta.

This is best done with a calculator.

Exercise:  Find the length of the curve r = 5(1 + cos(theta)) between 0 and 2pi.

V.  Surface Area of Revolution

We have the following two formulas:

If r = r(theta) is revolved around the polar axis (x-axis) then the Surface area is

If it is revolved around the y-axis then the resulting surface area is

Exercise:  Use your graphing calculator to find the area the results when r = 1 + cos(theta) is revolved around the y-axis.