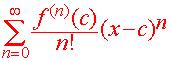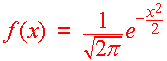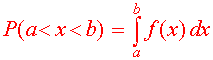Taylor Series
Taylor Series
Recall that the Taylor polynomial of degree
n for a differentiable function
f(x) centered
at x = c is
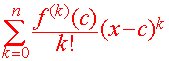
If we let n approach infinity, we arrive at the Taylor Series for f(x)
centered
at x = c.
|
Definition The Taylor Series for f(x) centered at x = c is
|
If c = 0 we call this series the Mclaurin Series for
f(x). Recall that the error of the nth degree Taylor Polynomial is given
by
f (n+1)(z)
R =
(z - c)n+1
(n + 1)!
Hence if
then the Taylor Series converges.
Example
Find the McLaurin Series expansion for
f(x) = cos(x)
Solution
We construct the following table.
| n | f (n)(x) | f (n)(0) |
| 0 | cos x | 1 |
| 1 | -sin x | 0 |
| 2 | -cos x | -1 |
| 3 | sin x | 0 |
| 4 | cos x | 1 |
| 5 | -sin x | 0 |
| 6 | -cos x | -1 |
Hence we have the series
x2
x4 x6
x8
1 -
+
-
+
- ...
2!
4!
6! 8!
Notice that the series only contains even powers of x and even
factorials. Even numbers can be represented by 2n. Also notice
that this is an alternating series, hence the McLaurin series is
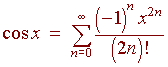
Exercises Find the Taylor series expansion for
-
sin(x) centered at x = p/2
-
sinh(x) centered at x = 0
Statistics
The Standard Normal Distribution function is defined by
|
Normal Distribution Function
|
We define the probability as follows:
|
Definition of Probability
|
Example:
Use McLaurin series and the fact that
to approximate the probability of getting a "B" in this
class if the average is 70 and the standard deviation is
10 and the instructor grades on a
"curve". A "B" corresponds to between 1 and
2 standard deviations from the mean, hence
we need to compute
We can calculate the first many terms on the calculator to get an approximate value of
0.76
In the first quarter you learned a proof that
In the second quarter you used L'Hopitals rule. Now we will do it a
third way: We have
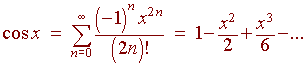
Hence
x2 x3
1 - cos x =
- + ...
2 3
Now divide both sides by x to get
1 - cos x
x x2
=
- + ...
x
2 3
When x = 0, the right hand side becomes zero,
hence so does the left hand side.
Exercise
Prove L'Hopital's Rule using power series.
Addition and Subtraction of Power
Series
|
Theorem |
Example:
We have that the power series representation of
1
ln(1
- x) +
1 - x
is
Exercise
Find the power Series Representation for
arctan x
+ arctanh x
Multiplication of Power Series
Suppose we have two power series
and
What is the power series for
f(x)g(x)
Consider the following example. Let
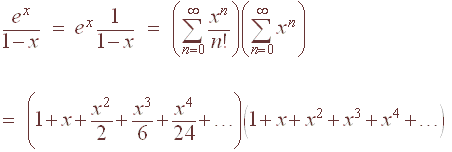
We can multiply these series as though they were finite series. We
collect the coefficients:
-
The constant term is 1.
-
The first degree term is 1 + 1 = 2.
-
The second degree term is 1 + 1 + 1/2 = 5/2.
-
The third degree term is 1 + 1 + 1/2 + 1/6 = 8/3
-
The fourth degree term is 1 + 1 + 1/2 + 1/6 + 1/24 = 65/24
We can continue this process indefinitely, or better yet use a computer to generate the terms.
The series is
5
8
65
1 + x +
x2 +
x3 +
x4 + ...
2
3
24
Division of Power Series
Suppose we want to find the power series representation of
We multiply by the denominator and equate coefficients:
(c0 + c1x + c2x2 + ...)(1
+ x + x2/2 + x3/6 + x4/24 + ...) =
(x - x3/3 + x5/5- x7/7 +...)
-
The constant coefficient gives us c0 = 0.
The first degree term gives us c0 + c1 = 1. Hence c1 = 1.
-
The second degree term gives us 1 + c2 = 0. Hence c2 = -1.
-
The third degree term gives us 1/2 - 1 + c3 = -1/3. Hence c3 = 1 - 1/2 - 1/3 = 1/6.
and so on.
The series is
1
x - x2 +
x3 + ...
6
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions