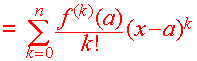Taylor Polynomials

Review of the Tangent Line

 Recall that if f(x) is a function, then f '(a) is the slope of the tangent line at x = a.  Hence

        y - f(a) = f '(a) (x - a)  

or

        P1(x)  =  y  =  f(a) + f '(a) (x - a) 

is the equation of the tangent line.  We can say that this is the best linear approximation to f(x) near a.

Note:      P1'(a) = f '(a).

Quadratic Approximations

Example

Let 

        f(x) = e2x

Find the best quadratic approximation at  x = 0.

Solution  

Note 

        f '(x) = 2e2x  

and 

        f ''(x) = 4e2x
Let 

        P2(x)  =  a0 + a1x + a2x2  

Take derivatives we obtain 

        P'2(x) = a1 + 2a2x  

and 

        P''2(x) = 2a2
We want the derivatives of f and P to match up.  We have

        P2(0)  =  a0  =  f(0)  =  1 

Hence 

        a0 = 1
         
Next

        P2'(0)   =  a1  =  f '(0)  =  2 

Hence

        a1 = 2

Finally


        P2''(0) = 2a2 = f ''(0) = 4 

Hence  

        a2 = 2

So

        P2(x) = 1 + 2x + 2x2
       
        
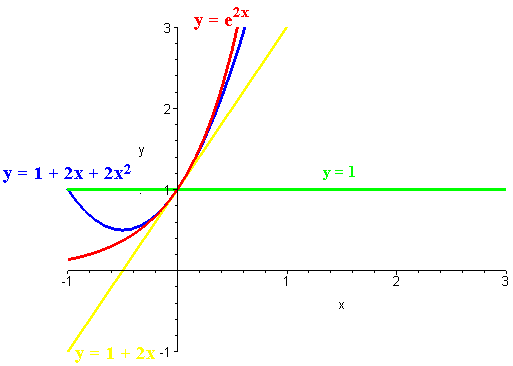
Notice that the tangent line approximates the curve well for values near x = 0, however the quadratic approximation is a better fit near this point.  This leads us to the idea of using higher degree polynomials to get even better fitting curves.

 

The Taylor Polynomial


Suppose that we want the best nth degree approximation to f(x) at x = a.  We compare f(x) to

        Pn(x) =  a0 + a1(x - a) + a2(x - a)2  + a3(x - a)3 + ... + an(x - a)n

We make the following observations:

        f(a)  =  Pn(a)  =  a0  
so that  

        a0  =  f(a)
Now we investigate the first derivative.

        f '(a)  =  P'n(a)  =   a1 + 2a2(x - a)  + 3a3(x - a)2 + ... + nan(x - a)n-1 at x = a 

so that 

        a1 = f '(a)

Taking second derivatives gives

        f ''(a) = P''n(a) =   2a2 + (3)(2)a3(x - a)+ ... + n(n - 1)an(x - a)n-2 at x = a 

so that 

                    1
        a2 =           f ''(a)
                    2

Note Each time we take a derivative we pick up the next integer in other words
        
                     1
        a3 =              f '''(a)
                  (2)(3)


If we define f(k)(a) to mean the kth derivative of f evaluated at a  then

                     1
        ak  =              f (k) (a)
                     k!

We now have the key ingredient for our main result.

                         The Taylor Polynomial
The nth degree Taylor polynomial at x = a is

                                            f ''(a)                      f (3)(a)                         f (n)(a)    
Pn(x) =  f(a) + f '(a)(x - a) +              (x - a)2  +              (x - a)3 + ... +              (x - a)n
                                              2!                          3!                                  n!

        



The special case when a = 0 is called the McLaurin Series
          The McLaurin Polynomial

The McLaurin Polynomial of a differentiable function f(x) is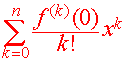 

         


Examples:

Find the fifth degree McLaurin Polynomial for sin x.  

Solution

We construct the following table to assist in finding the derivatives.

        
k f (k)(x) f (k)(0)
0 sin x 0
1 cos x 1
2 -sin x 0
3 -cos x -1
4 sin x 0
5 cos x 1

Now put this into the formula to get 

                               1              0               -1                0               1
        P5(x) = 0  +          x  +           x2  +          x3  +          x4  +          x5  
                              1!             2!               3!               4!              5!

                      x3           x5     
        =  x  -            +           
                      6          120

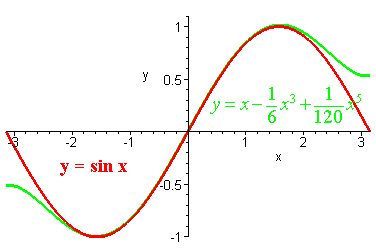
Notice how well the McLaurin polynomial  (in green) approximates y = sin x (in red) for on period.
       

 

Taylor's Remainder

Taylor's Remainder Theorem says that any smooth function can be written as an nth degree Taylor polynomial plus a function that is of order n + 1 near x = c.

          Taylor's Remainder Theorem

If f is smooth from a to b, let Pn(x)  be the nth degree Taylor polynomial at x = c, then for every x there is a z between x and c with

                                   f (n+1)(z)       
          f(x) = Pn(x) +                     (x - c)n+1   
                                   (n + 1)!

 


Example

We have

                                   (0.1)3     (0.1)5     sin z
        sin(0.1)  =  0.1  -            +           -           (0.1)6  =  .099833416667 + E
                                      6          120         6!

  Where 

                   1
        E  <          (.1)6  = .0000000014
                  6!

We see that the error quite small.

 

Back to the Series Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions