Creating Power Series From Functions

The Geometric Power Series

Recall that

       

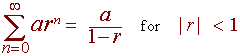
Substituting x for r, we have 
 
       

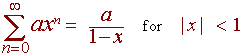
We write

Milking the Geometric Power Series

By using substitution, we can obtain power series expansions from the geometric series.

Example 1  

Substituting x² for x, we have 

       

Example 2  

Multiplying by x we have

Example 3  

Suppose we want to find the power series for 

                          1
        f(x)  =                    
                      2x - 3

centered at x = 4.  We rewrite the function as 

                    1                            1
                                    =                     
          2(x - 4) + 8 - 3          2(x - 4) + 5

       

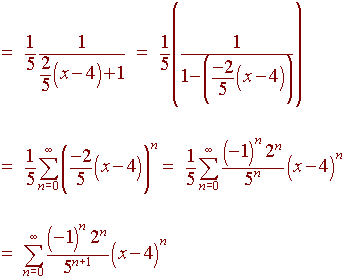
Example 4  

Substituting -x for x, we have

       

Example 5  

Substituting x² in for x in the previous example, we have

       

Example 6  

Taking the integral of the previous example, we have

       

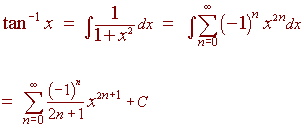
Exercise  Find the power series that represents the following functions:

1. ln(1 + x)
   

2. tanh^-1x
   

3. -(1 - x)^-2 
   

Integrating Impossible Functions

We can use power series to integrate functions where there are no standard techniques of integration available.


Example:  

Use power series to find the integral 

       

Then use this integral to approximate 

       

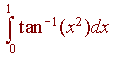
Solution:   

Notice that this is a very difficult integral to solve.  We resort to power series.  First we use the series expansion from Example 6, replacing x with x².  

       

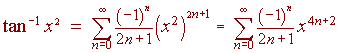
Integrating we arrive at the solution 

      

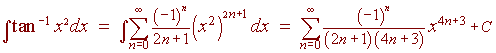
Now to solve the definite integral, notice that when we plug in 0 we get 0, hence the definite integral is

       
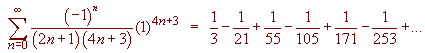
Using the first 5 terms to approximate this we get 0.300

Notice that the error is less than the next term (which comes from x²³/253)

        E < 1/253  =  .004.

Back to the Series Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions