Polar Coordinates

Definition of Polar Coordinates

Recall that we define a point (x,y) on the plane as x units to the right of the origin and y units to the left of the origin.  This works great for lines and parabolas, but circles have somewhat messy equations.  As an alternative we define a new coordinate system where the first coordinate r is the distance from the origin to the point and the second coordinate q is the angle that the ray from the origin to the point makes with the positive x-axis.  From trigonometry, we have

x = rcosq     y = rsinq


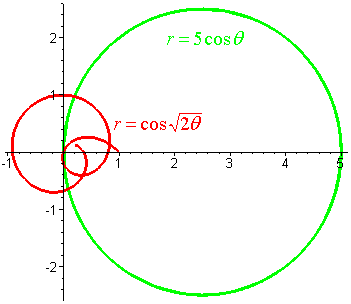
Your calculator has a special mode for polar coordinates.  We use the calculator to graph

        r = 5cosq  

and 

        r = cos( )

       

 

Circles

A circle centered at the origin has equation

        x2 + y2 = R2

In polar form we have

        r = R

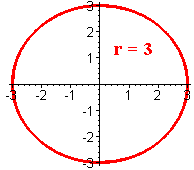
For example the circle of radius 3 centered at (0,0) has polar equation

        r = 3

 Lines

If 

        y = mx + b 

we can write

        r sin(q) = m r cos q + b 

or

                            b
        r  =                                    
                   sin q  -  m cos q

Conic Sections

Recall that a conic section is defined as follows:
Let f ( called the focus) be a fixed point in the plane, m (called the directrix) be a fixed line, and e (called the eccentricity) a positive constant.  Then the set of points P in the plane with

      |PF| 
                =   e
      |Pm|

is a conic section.  If e < 1 then the section is an ellipse, if e = 1, then its a parabola, 
and if e = 0 then it is a hyperbola.

Note:   If F is the origin m is x = d then

        |PF| = r,     |Pm| = d - r cos q 

so that the equation becomes

        r = e(d - rcos(q)) = ed - recos(q)

or

                   ed
  r   =                       
              1 + e cosq

 


Derivatives in Polar Coordinates

Theorem  

Let r = r(q) represent a polar curve, then

  dy              dy/dq                  r' sinq + r cosq
           =                      =                                       
  dx              dx/dq                  r' cosq - r sinq


           dy             r' sinq + r cosq
                        =                                                 
              dx                r' cosq - r sinq


Proof:  

Since 

        x = r cosq,     and     y = r sinq,

we can substitute in r = r(q) to get

        x = r cosq

Taking a derivative,


        x' = r' cosq - r sinq

and

        y' = r' sinq + r cosq.

Since 

         dy              dy/dq
                  =                                
         dx              dx/dq


dividing gives the result.


Example

Let

        r = q sinq

Then

        dy              (sinq + q cosq) sinq  +  q sinq cosq
                 =                                                                                  
        dx               (sinq + qcosq) cosq  - q sinq sinq


                          sin2q + 2qsinqcosq
        =                                                                              
                      sinq cosq + qcos2q - qsin2q


                   sinq cosq + qcos(2q)
        =                                                               
                    sin2q + qsin(2q)

 

Back to the Polar and Parametric Equations Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions