Conic Sections
Definition of the Conic Sections
Let e > 0 (called the eccentricity) and let
F be a point (called
the Focus) in the plane and let l be a fixed line (called the
directrix). Then a conic is the set of points,
P, such that
|
|

Where PF is the distance from the point to the focus and d(Pl) is the distance
from the point to the line.. We have the following classification:
| e | Type |
| 0 | circle |
| 0< e <1 | ellipse |
| 1 | parabola |
| e > 1 | hyperbola |
The Circumference of an Ellipse
Example
Find the circumference of the ellipse
x2 y2
+ = 1
4 9
Solution: We can solve for y
![]()
Soon we will see it is a square that we want so that we can ignore the sign.
![]()
So that
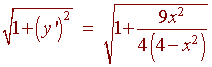
Now the find the length, we integrate this equation from 0
to 2 and then multiply by
4.
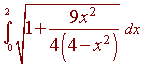
To attempt to solve this integral we let
x = 2 sin q,
dx = 2 cos q
The integral reduces to
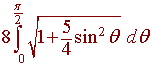
This integral is anything but elementary, but we can approximate it
with a computer as
15.87
and doubling it gives
31.74
Back to the Polar and Parametric Equations Page
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions