Polar Coordinates
Definition of Polar Coordinates
Recall that we define a point (x,y) on the plane as
x units to the right
of the origin and y units to the left of the origin. This works great
for lines and parabolas, but circles have somewhat messy equations. As
an alternative we define a new coordinate system where the first coordinate
r is the distance from the origin to the point and the second coordinate q
is the angle that the ray from the origin to the point makes with the
positive x-axis. From trigonometry, we have
|
x = rcosq y = rsinq |
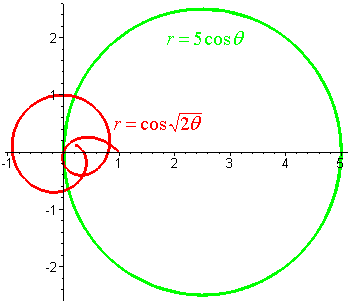
Your calculator has a special mode for polar coordinates. We use
the calculator to graph
r = 5cosq
and
r = cos(![]() )
)
A circle centered at the origin has equation
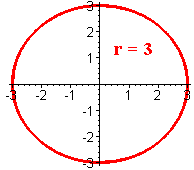
x2 + y2 = R2
In polar form we have
r = R
For example the circle of radius 3 centered at (0,0) has polar equation
r = 3
If
y = mx + b
we can write
r sin(q) =
m r cos q + b
or
b
r =
sin q - m cos q
Conic Sections
Recall that a conic section is defined as follows:
Let f ( called the focus) be a fixed point in the plane,
m (called the
directrix)
be a fixed line, and e (called the eccentricity) a positive constant. Then
the set of points P in the plane with
|PF|
= e
|Pm|
is a conic section. If e < 1 then the section is an ellipse, if
e = 1, then its a
parabola,
and
if e = 0 then it is a hyperbola.
Note: If F is the origin m is
x = d then
|PF| = r, |Pm| = d -
r cos q
so that the equation becomes
r = e(d - rcos(q)) = ed -
recos(q)
or
|
ed |
Derivatives in Polar Coordinates
Theorem
Let r = r(q) represent a polar curve, then
dy
dy/dq r' sinq
+ r cosq
=
=
dx
dx/dq
r' cosq
- r sinq
|
dy r' sinq
+ r cosq |
Proof:
Since
x = r cosq,
and y = r sinq,
we can substitute in r = r(q) to get
x = r cosq
Taking a derivative,
x' = r' cosq -
r sinq
and
y' = r' sinq +
r cosq.
Since
dy
dy/dq
=
dx
dx/dq
dividing gives the result.
Example
Let
r = q
sinq
Then
dy
(sinq
+ q cosq) sinq
+ q sinq cosq
=
dx
(sinq
+ qcosq) cosq
- q sinq sinq
sin2q + 2qsinqcosq
=
sinq cosq +
qcos2q - qsin2q
sinq cosq
+ qcos(2q)
=
sin2q
+ qsin(2q)
Back to the Polar and Parametric Equations Page
Back to the Math 107 Home Page