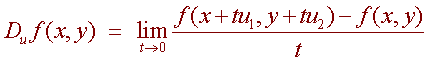
The Gradient

Directional Derivatives

Suppose you are given a topographical map and want to see how steep it is from a point that is neither due West or due North.  Recall that the slopes due north and due west are the two partial derivatives.  The slopes in other directions will be called the directional derivatives.  Formally, we define

Definition   Let f(x,y) be a differentiable function and let u be a unit vector then the directional derivative of f in the direction of u is

Note that if u is i then the directional derivative is just f_x and if u is j the it is f_y.

Just as there is a difficult and an easy way to compute partial derivatives, there is a difficult way and an easy way to compute directional derivatives.

Theorem Let f(x,y) be a differentiable function, and u be a unit vector with direction q, then

Example:  

Let 

        f(x,y)  =  2x + 3y² - xy 

and 

        v  =  <3,2> 

Find 

        D_v f(x,y)

Solution

We have 

        f_x  =  2 - y 

and 

        f_y  =  6y - x 

and 

       

Hence

        D_v f(x,y)  =  <2 - y, 6y - x> ^. <3/, 2/> 

                  2                         3      
        =                (2 - y)  +            (6y - x)
                                   

Exercise

Let 

       

Find  D_v f(x,y)

The Gradient

We define 

grad f  =  <fx, fy>

Notice that
  
       

Du f(x,y) = (grad f) . u

The gradient has a special place among directional derivatives.  The theorem below states this relationship.

Theorem If grad f(x,y) = 0 then for all u,  Du f(x,y) = 0 The direction of grad f(x,y) is the direction with maximal directional derivative. The direction of -grad f(x,y) is the direction with the minimal directional derivative.

Proof:  

1. If 
   
           gradf(x,y)  =  0 
   
   then   
   
           D_u f(x,y)  =  grad f ^. u  =  0 ^. u  =  0
   

2. D_u f(x,y)  =  grad f ^. u  =  ||grad f || cos q
   
   This is a maximum when q = 0 and a minimum when q = p.  If q = 0 then grad f and u point in the same direction.  If q = p then u and grad f point in opposite directions.  This proves 2 and 3.
   

Example:   

Suppose that a hill has altitude 

        w(x,y)  =  x² - y

Find the direction that is the steepest uphill and the steepest downhill at the point (2,3).

Solution

We find

        grad w  =  <2x, -y>  =  <4, -3>

Hence the steepest uphill is in the direction 

        <4,-3>

while the steepest downhill is in the direction 

        -<4,-3>  =  <-4,3>

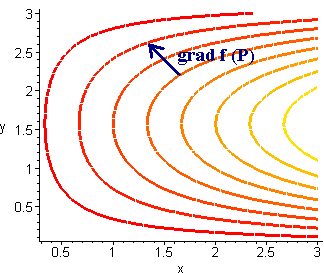
The Gradient and Level Curves

If f is differentiable at (a,b) and grad f is nonzero at (a,b) then grad f is perpendicular to the level curve through (a,b).

Back to the Functions of Several Variables Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions

This site has had visitors since February 26, 2001