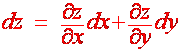Differentials
The Total Differential
In single variable calculus, we discussed the idea of the differential. We now define the differential for functions of two
variables.
|
Definition Let z = f(x,y) then the total differential for z is
|
Example
For
z = f(x,y) = x2 + xy
the definition produces
dz = (2x + y) dx + x dy
Exercise
Find dz if
z = x siny cosy
Application
In Chemistry we learn that
PV = NRT
where NR is a constant. We can
write:
PV
T =
= k PV
NR
Suppose at 25 degrees C, gas is in an expanding cylinder of
55cc at a pressure
of 3 atm. Also suppose that the pressure is increased by
0.1 atm and
the volume is decreased by 0.05 cc. Then
dT = kPdV + kVdP
@
k [(3)(-0.05) + 50(0.1)) = 0.35k
so that there is an increase on the temperature of about k(0.35) degrees
C
Suppose that you measured the dimensions of a tin can to be
h = 6
![]() 0.1 inch
0.1 inch
and
r = 2
![]() 0.05 inch
0.05 inch
What is the approximate error in your measurement for the volume of the can?
Solution
We have
V = pr2
h
Hence the error can be approximated by
DV
@ 2prh Dr
+ pr2 Dh
= 2p(2)(6)(0.5) +p(4)(.1)
= 1.2 p
+ .4 p = 1.6 p @
5.0 cu inches
Hence the volume is
V = 75.4
![]() 5 cu inches
5 cu inches
Differentiability
Theorem: |
More informally, if
z
= f(x,y)
is a differentiable function at the origin of two variables then
z = Ax + By +
error
where the error term is small near the origin. In other words the graph is approximately equal to a plane near the origin.
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions