Locating and Classifying Local Extrema

Definition of Relative Max and Min

We now extend the definition of relative max and min to functions of two variables.

Definition 1.  A function f(x,y) has a relative maximum at (a,b) if there is a       d-neighborhood centered at (a,b) such that            f(a,b)  >  f(x,y) 2. There is a relative minimum at (x,y) if            f(a,b)  <  f(x,y)     for all (x,y) in the d- neighborhood.

For differentiable functions of one variable, relative extrema occur at a point only if the first derivative is zero at that point.  A similar statement holds for functions of two variables, but the gradient replaces the first derivative.

Theorem   If f(x,y) has a relative maximum or minimum at a point P,       grad f(P)  =  0

Example   

Let 

        f(x,y)  =  x² + xy - 2y + x - 1

then 

        grad f  =  <2x + y + 1, x - 2>  =  0

so that 

        x - 2  =  0

 or 

        x  =  2

Hence

        2(2) + y + 1  =  0  

so 

        y  =  5

A possible extrema is (2,-5).

Notice that just as the vanishing of the first derivative does not guarantee a maximum or a minimum, the vanishing of the gradient does not guarantee a relative extrema either.  But once again, the second derivative comes to the rescue.  We begin by defining a version of the second derivative for functions of two variables.

Definition We call the matrix           the Hessian and its determinant is        D  =  fxxfyy  -  fxy2

Now we are ready to state the second derivative test for functions of two variables.  This theorem helps us to classify the critical points as maximum, minimum, or neither.  In fact their is a special type of critical point that is neither a maximum nor a minimum, called a saddle point.  A surface with a saddle point is locally shaped like a saddle in that front and back go upwards from the critical point while left and right go downwards from the critical point.

Theorem (Second Derivative Test For Functions of Two Variables) If grad f = 0 we have the following D fxx Type > 0 > 0 Rel Min > 0 < 0 Rel Max < 0 any Saddle = 0 any Test Fails

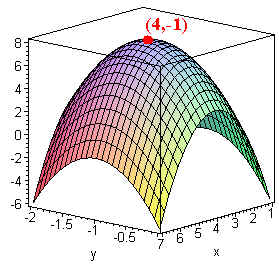
Example:

Let 

        f(x,y)  =  -x² - 5y² + 8x - 10y - 13   

then 

        grad f  =  <-2x + 8, -10y - 10>  =  0     at     (4, -1)

we have 

        f_xx  =  -2       f_yy  =  -10       and       f_xy  =  0 

Hence

        D  =  (-2)(-10) - 0  >  0

so f has a relative maximum at (4,-1)

Example:  Let

        f(x,y)  =  4xy - x⁴ - y⁴

then 

        grad f  =  <4y - 4x³, 4x - 4y³>

We solve:

        4y - 4x³  =  0 

so that 

        y  =  x³  

Hence 

        4x - 4(x³)³  =  0

or

        x - x⁹  =  0 

so that 

        x = 1      or      x = 0      or      x = -1

plugging these back into 

        y  =  x³  

gives us the points 

        (1,1)      (0,0)      and      (-1,-1)

We have 

        f_xx  =  -12x²        f_yy  =  -12y²        and        f_xy  =   4

Hence 

        D = 144x²y² - 16

We write the table:

Point	D	fxx	Type
(1,1)	128	-12	Max
(0,0)	-16	0	Saddle
(-1,-1)	128	-12	Max

Minimizing Distance

Example

Find the minimum distance from the point (2,1,4) to the plane

        x + 2y + z = 5

Solution:  

We minimize the square of the distance so that we do not have to deal with messy roots.

        S  =  (x - 2)² + (y - 1)² + (5 - x - 2y - 4)²

We take the gradient and set it equal to 0.

        <2(x - 2) - 2(5 - x - 2y - 4), 2(y - 1) - 2(5 - x - 2y - 4)>  =  0

so

        2x - 4 - 10 + 2x + 4y + 8  =  0    

and

        2y - 2 - 10 + 2x + 4y + 8  =  0

simplifying gives

        4x + 4y - 6 = 0    and    2x + 6y - 4 = 0
or
        2x + 2y - 3 = 0    and    2x + 6y - 4 = 0

subtracting the first from the second, we get:

        4y - 1  =  0 

so 

        y  =  1/4

Plugging back in to any of the original equations gives

        x = 7/4

Finally, we have

        s = (7/4 - 2)² + (1/4 - 1)² + (5 - 7/4- 2(1/4) - 4)²  =  35/16  =  2.1875

Taking the square root gives that minimum distance of 1.479.  Note that by geometry, this must be the minimum distance, since the minimum distance is guaranteed to exist.

The Least Squares Regression Line

Example:

Suppose you have three points in the plane and want to find the line 

        y = mx + b 

that is closest to the points. Then we want to minimize the sum of the squares of the distances, that is find m and b such that

        d₁² + d₂² + d₃² 

is minimum.  We call the equation 

        y = mx + b

the least squares regression line.  We calculate

        d₁² + d₂² + d₃²  =  f  =  (y₁ - (mx₁+ b))² + (y₂ - (mx₂+ b))² + (y₃ - (mx₃+ b))²  

To minimize we set

        gradf  =  <f_m, f_b>  =  0  (Notice that m and b are the variables)

Taking derivatives gives

        f_m  =  2(y₁ - (mx₁+ b))(-x₁) + 2(y₂ - (mx₂+ b))(-x₂) + 2(y₃ - (mx₃+ b))(-x₃)  =  0

and

        f_b  =  -2(y₁ - (mx₁+ b)) - 2(y₂ - (mx₂+ b)) - 2(y₃ - (mx₃+ b))  =  0   

We have after dividing by -2

1. x₁(y₁ - (mx₁+ b)) + x₂(y₂ - (mx₂+ b)) + x₃(y₃ - (mx₃+ b))  =  0    
   

2. (y₁ - (mx₁+ b)) + (y₂ - (mx₂+ b)) + (y₃ - (mx₃+ b))  =  0 
   

In S notation, we have

Notice here n = 3 since there are three points.  These equations work for an arbitrary number of points.

We can solve to get

     

and

A JAVA Applet that can find the equation and graph the line can be found here.

Exercise:  Find the equation of the regression line for

            (3,2)      (5,1)      and      (4,3)

Back to the Functions of Several Variables Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions