Definition
Let f(x,y)
be a differentiable function and let u
be a unit vector then the directional derivative of f
in the direction of u
is
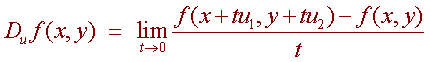
The Gradient
Directional Derivatives
Suppose you are given a topographical map and want to see how steep it is from a point
that is neither due West or due North. Recall that the slopes due north
and due west are the two partial derivatives. The slopes in other
directions will be called the directional derivatives. Formally, we
define
Definition |
Note that if u is i then the directional derivative is just
fx and
if u is j the it is
fy.
Just as there is a difficult and an easy way to compute partial derivatives,
there is a difficult way and an easy way to compute directional derivatives.
Theorem
|
Example:
Let
f(x,y) = 2x + 3y2 - xy
and
v = <3,2>
Find
Dv
f(x,y)
Solution
We have
fx = 2 - y
and
fy = 6y -
x
and
![]()
Hence
Dv f(x,y) =
<2 - y, 6y -
x> . <3/![]() ,
2/
,
2/![]() >
>
2
3
=
(2 - y) +
(6y - x)
![]()
![]()
Exercise
Let
![]()
Find Dv f(x,y)
The Gradient
We define
| grad f = <fx, fy> |
Notice that
| Du f(x,y) = (grad f) . u |
The gradient has a special place among directional derivatives. The
theorem below states this relationship.
|
Theorem
|
Proof:
If
gradf(x,y) = 0
then
Du f(x,y) =
grad f .
u = 0 . u = 0
Du f(x,y) = grad f . u =
||grad f || cos q
This is a maximum when q
= 0 and a minimum when
q = p. If q
= 0 then grad f and u point in the same direction. If
q
= p then u and
grad f point in opposite directions.
This proves 2 and 3.
Example:
Suppose that a hill has altitude
w(x,y) =
x2 - y
Find the direction that is the steepest uphill and the steepest downhill at the
point (2,3).
Solution
We find
grad w = <2x,
-1> = <4, -1>
Hence the steepest uphill is in the direction
<4,-1>
while the steepest downhill is in the direction
-<4,-1> = <-4,1>
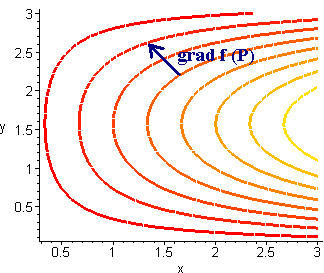
The Gradient and Level Curves
If f is differentiable at (a,b) and grad f is nonzero at (a,b) then grad f is perpendicular to the level curve through (a,b).
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page