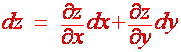Differentials

The Total Differential

 In single variable calculus, we discussed the idea of the differential.  We now define the differential for functions of two variables. 

          Definition

Let z = f(x,y) then the total differential for z is

         


Example

For 

        z  =  f(x,y)  =  x2 + xy

the definition produces

        dz  =  (2x + y) dx + x dy

Exercise  

Find dz if 

        z  =  x siny cosy

Application

In Chemistry we learn that 

        PV  =  NRT 

where NR is a constant.  We can write:

                    PV
        T  =                 =  k PV
                    NR

Suppose at 25 degrees C, gas is in an expanding cylinder of 55cc at a pressure of 3 atm.  Also suppose that the pressure is increased by 0.1 atm and the volume is decreased by 0.05 cc.  Then

        dT  =  kPdV + kVdP

        @  k [(3)(-0.05) + 50(0.1))  =  0.35k

so that there is an increase on the temperature of about k(0.35) degrees C

Error

Suppose that you measured the dimensions of a tin can to be

        h  =  6 0.1 inch 
and

        r  =  2 0.05 inch

What is the approximate error in your measurement for the volume of the can?

Solution

We have 

        V  =  pr2 h  

Hence the error can be approximated by

        DV  @  2prh Dr + pr2 Dh  =  2p(2)(6)(0.5) +p(4)(.1)
        = 1.2 p + .4 p = 1.6 p @ 5.0 cu inches

Hence the volume is

        V  =  75.4 5 cu inches

 

Differentiability



               Theorem: 
If a function f(x,y) is differentiable at a point (a,b) then it is continuous at (a,b) where differentiable means

          Df(x,y) = fx(a,b)Dx + fy(a,b)Dy + e1Dx + e2Dy

where both e1 and e2 approach 0 as Dx and Dy approach 0.  Furthermore if the partial derivatives are continuous then the function is differentiable. 

 

More informally, if

        z  =  f(x,y)

is a differentiable function at the origin of two variables then

        z = Ax + By + error

where the error term is small near the origin.  In other words the graph is approximately equal to a plane near the origin.

 

Back to the Functions of Several Variables Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions