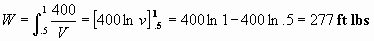Work Part 2

1. Quiz
   

2. Homework
   

3. Emptying a tank
   Suppose that a cylindrical tank of water with radius 10 and height 20 is pumped out fully.  How much work is required?
   
   Solution:

   F = weight = (density)(volume) = (64 lbs per cu ft)p r² h cu ft = 64p(100)d y

   The distance that water y feet above the ground must be pumped is 20 - y feet.

   We have

   
   

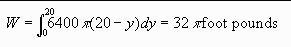
4. Lifting a Chain

   A 2,000 lb car has gone over a 100 foot cliff at the pass.  A crane lifts up to car with a chain that is 10 lbs per foot.  How much work is done?  

   Solution:  Work = Work for the car + Work for the chain

   Work for the car = 2,000(100)

   Work for the chain =

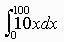
   Since the force is 10 times the distance the chain link is from the top.

   This integral is 50,000.   Hence the total work is

   200,000 + 50,000 = 250,000 ft lbs.
   

5. Running an Automobile

   An automobile is run by a piston which turns the wheel.  We have the equation

   Force = pressure (lbs/sq inch) times Volume ( cu inches) = pressure(p r²)

   Boyle's Law states that the pressure is inversely proportional to the volume:  

   P = k/V

   Hence

   

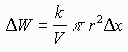
   But  p r²D x = D V

   Hence the total work is

   

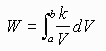
   Example:  Suppose a piston has gas filled initially to a volume of .5 cu ft and a pressure of 800 lbs/sq ft.  The piston expands to a volume of 1 cu ft.  Find the work done by the gas.

   Solution:  We have P = k/v;  800 = k/.5;  k = 400