Cylindrical Shells

I.  Cylindrical Shells

Consider rotating the region between the curve y = x², the line x = 2 and the x -axis about the y-axis.  If instead of taking a cross section perpendicular to the y-axis, we take a cross section perpendicular to the x-axis, and revolve it about the y-axis, we get a cylinder.  Recall that the area of a cylinder is given by:

A = 2p r h

where r is the radius of the cylinder and h is the height of the cylinder.  We can see that the radius is the x coordinate of the point on the curve, and the height is the y coordinate of the curve.  Hence A(x) = 2pxy = 2px(x²)

Therefore the volume is given by

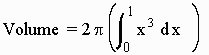
Example:   Find the volume of revolution of the region bounded by the curves y = x² + 2 and y =  x + 4 about the y axis.

Solution:

We draw the picture with a cross section perpendicular to the x-axis.  The radius of the cylinder is x and the height is the difference of the y coordinates:  (x + 4) - (x² + 2).  We solve for a and b.  (x + 4) = (x² + 2).  x² - x - 2 = 0 .  (x - 2)(x + 1) = 0.  So that a = -1 and b = 2.  Hence the volume is equal to

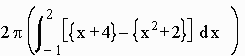
Exercises:  

Students will try:

A)  y = x² + x - 2, y = 0 about the y-axis

B)  y = x² - 3x + 2, y = 0 about the y-axis

C)  x = 1 - y² , x = 0 about the x-axis

D)  y = xsqrt(1 + x³), y = 0, x = 0, y = 2 about the y-axis

E)  x²  + (y - 1)²  = 1 about the y-axis

F)  x²  + (y - 1)²  = 1 about the x-axis

G)  y = x² -2x + 1 about the line x = 3

H)  y = 3x² - 2x + 1 about the line y = 3