The Second Fundamental Theorem of Calculus

I.  Quiz

II.  Homework

III.  The Mean Value Theorem For Integrals

Let f be continuous on [a,b] then there is a c in [a,b] such that

int from a to b of f(x) dx = f(c)(b - a)

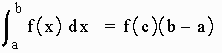
We define the average value of f(x) between a and b as

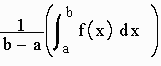
Example: The average value of sin x between 0 and pi is

1/(pi - 0)int from 0 to pi of sinx dx = 1/(pi - 0)[-cosx]from 0 to pi

= (1/pi)(1 + 2) = 2/pi

V.  The Second Fundamental Theorem of Calculus

Let f be continuous on [a,b] then

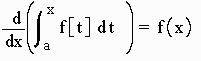
A Proof will be given in class.

Exercise:

d/dx int from 3 to x of t^t = x^x

Exercise:

d/dx int from 5 to x² of sqrt(1 + t² )dt    let y = int from 5 to u of sqrt(1 + t² )dt  and u = x²

then dy/dx = dy/du du/dx = sqrt(1 + u²)(2x) = sqrt(1 + x⁴ )2x. 

Example:  Let

If g(x) is the inverse of f(x), find g'(0)

Solution:  We can use the formula

g'(0) = 1/f'(g(0)

By the second fundamental theorem of calculus, f'(x) = sin²(x).  To find g(0) we note that an integral is 0 when a = b.  Hence g(0) = 3.  Finally

g'(0) = 1/f'(3) = 1/sin²(3) approx 50.