Discs and Washers Part 2

I.  Quiz

II.  Homework

III.   Revolving about a non-axis line.

Find the volume of the region formed by revolving the curve y = x³  0<x<2 about the line y = -2.

Solution: This time we revolve the cross-section and obtain a disk.  The radius of the disk is 2 plus the y coordinate of the curve.  Hence

A = p(2 + x³)² 

so that

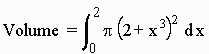
Example:

Try revolving the curve y = x² from 0 to 2 about the line x = 5

We have

A = p[(5 - sqrt(y))² - 9]

so that

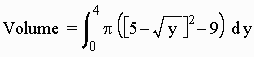
IV.  Applications of Volume

Example:  The Volume of the Khufu Pyramid

The base of the Khufu pyramid is a square with wide length 736 feet and the angle that the base makes with the ground is 50.8597 degrees.  Find the volume of the Khufu pyramid.

Solution:  First note that we need to change to radian measure.  

50.8597 degrees = .88767 radians.  

The height of the pyramid is 736tan(.88767) = 904.348

We have that the area of a cross section is s² where s is the side length of the square.  

Placing the y-axis through the top of the pyramid and the origin at the middle of the base, we have that s = sqrt(2) x

Hence A(x) = 2x².  Since the axis perpendicular to the cross sections is the y-axis, we need A in terms of y.    

We set up similar triangles:

x/736 = y/904.348

x = .8138y

Hence A(y) = 1.3247x²

We calculate

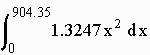
= 361131 cubic feet.

Example:  Volume of a Sphere

A sphere is formed by rotation the curve

y = sqrt(r² - x²)

We have

Volume =

= p[r²x - x²/3]|from -r to r  =  p[(r³ -  r³ /3) - (-r³ -  -r³ /3) = 4/3 p r³

Exercise:  Two cylinders of radius r intersect each other at right angles.  Find the volume of their intersection.

Hint:  Consider cross sections parallel to both axes of rotation.  These cross sections are squares.  Then show that the side length is 2sqrt(r² - x²)  

Click here for the cored sphere