I.  Homework

II.  Area of a rectangle and using rectangles to approximate area under a curve

Recall that the area of a rectangle is the height times the base.  What if we wanted to paint a wall that has a ceiling the shape of y = x² , a flat floor and a right wall at x = 2 yards and a left wall at x = 5 yards.

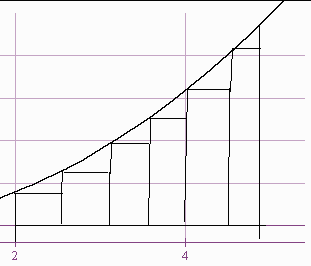
 We can approximate the area by cutting out 6 rectangles.  Since the base of the wall is 5 - 2 yards long, and there are 6 rectangles, the base of each rectangle is (5 - 2)/6 = .5 yards.  The height of each rectangle is the y-coordinate of the left side of each rectangle.  The x- coordinates are

2 + 0(.5),2 + 1(.5), 2 + 2(.5), 2 + 3(.5), 2 + 4(.5), 2 + 5(.5) so that the y coordinates are

(2 + 0(.5))²,(2 + 1(.5))², (2 + 2(.5))², (2 + 3(.5))², (2 + 4(.5))², (2 + 5(.5))²

We see that the i^th rectangle has y coordinate:

height = (2 + i(.5))² = 2 + 2i + .25i²

To get the area of the i^th rectangle we multiply the height by the base:

(2 + 2i + .25i²)(.5)

Finally to get the total area we add the terms up:

sum[(2 + 2i + .25i²)(.5)]

This will be a lower bound for the area.  

Learn the following formulas:

1)  sum[c] = cn

2)  sum[i] = n(n + 1)/2

3)  sum[i²] = n(n + 1)(2n + 1)/6

4)  sum[i³] = n²(n + 1)²/4 

Hence:  sum[(2 + 2i + .25i²)(.5)] = .5sum[2] + sum[i] + .125sum[i²]

= .5(10) + (5)(6)/2 + .125(25)(36)/2

In general the area under a curve y = f(x) is defined as

lim as n approaches infinity sum from i = 1 to n of f(a + i(b - a)/n))(b - a)/n

In our example, we have

lim sum from i = 1 to n of (2 + 3i/n)²(3/n)

= lim (3/n) sum of 4 + 18i/n + 9i²/n²

= lim[(3/n sum 4) + (54/n² sum i) + 27/n³ sum i²]

=   lim[(3/n (4n)) + (54/n² (n)(n + 1)/2) + 27/n³ n(n + 1)(2n + 1)/6]

=12 + 27 + 27(2)/6 = 48

III.  The Definite Integral

Definition:  Let a = x₀, x₁, ...x_n = b be a partition of [a,b] and let    

x_i-1 <   c_i <    x_i  

then

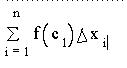
is called a Reimann Sum, and the lim as the maximum delta x_i  approaches 0 is called the definite integral.  

Note:  f(x) can be negative

Usually to compute a definite integral, we use left or right sums.

Example

Find int from 1 to 3 of 2x + 1 dx

Solution:  The right sum is sum [(2(1 +i(3-1)/n)+1)(3-1)/n

=  sum [(3 +4i/n)(2/n)]  = sum 6/n + 8/n²sum(i)

= (6/n)n +  8/n²(n(n + 1)/2) = 6 + 4[(n² +n)/n²] 

Taking the limit as n -> infinity we get 10

IV.  Special cases:

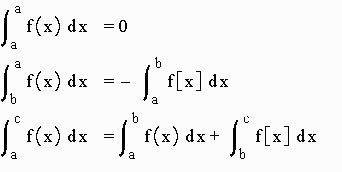
Example:

int from -2 to 3 of |x|dx = int from -2 to 0 of -x dx+ int from  0 to 3 of xdx

= -1/2 (2)(2) + 1/2(3)(3) = 5/2