Moments and Centroids

1. Mass and Slugs

   Newton's Law states that
   

   F = ma

   where F is the force, m is the mass, and a is the acceleration.  In the US system Force is measured in pounds and mass is measures in slugs.  

   Example:  I weigh 165 lbs.  What is my mass?

   Solution:  
   Since weight corresponds with gravitational force, and the acceleration of gravity is 32 ft/sec² we have

   165 = 32m

   or m = 5.15 slugs.

   In the metric system, kg is a mass unit and Newtons is a weight unit.
   

2. Moments and Center of Mass for Discrete Mass Points.

   Suppose that we have a teeter totter and a 10 kg child is on the left 5 meters from the center of the teeter totter and a 15 kg child is on the right 4 meters from the center of the teeter totter.  We define the moment as:

   10(-5) + 15(4) = 10

   In general, we define the moment for masses m_i  at the points x_i  to be

   Moment = S m_i x_i

   If the moment is 0 then we say that the system is in equilibrium.  Otherwise, let x be the value such that sum m_i (x_i - x) = 0.  Then x is called the center of mass of the system.

   Theorem:  x = moment/total mass

   Proof:  

   

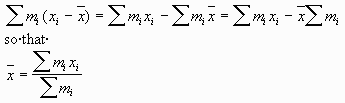
   Example:  Find the center of mass of the teeter totter.

   We have moment = 10 and the total mass = 25, hence the

   center of mass = 10/25 = .4

   We can say that if the center of the teeter totter was .4 meters from the current center, then the children would be in balance.

   For points in the plane, we can find moments and centers of mass coordinatewise.  We define:

   mx = moment about the x axis =  S mi xi my = moment about the y axis =  S mi yi Center of Mass = (my/m, mx/m)

   Example:  For the points (-3,0) with mass 4, (2,2) with mass 3, and (1,-2) with mass 1 we have

   m_x = (4)(-3) + (3)(2) + (1)(1) = -5

   m_y = (4)(0) + (3)(2) + (1)(-2) = 8

   Center of Mass = (-5/8,8/8) = (-.625,1)
   

3. Center of Mass for a two Dimensional Plate

   First, we recall that for a region of density p bounded by f(x) and g(x)
   

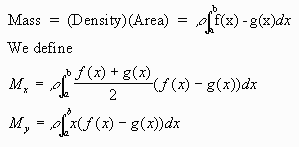
   and   

    

   center of mass = (my/m, mx/m)

   Example:  Find the center of mass for the plate of constant density 2 that is bounded by the curves y = 1 - x, y = 0 and x = 0

   We have

   
   

4. Pappus Theorem

   Suppose that we revolve a around the y-axis.  Then the volume of revolution is:

   V = 2prA where A is the area of the region and r is the distance from the centroid (constant density) to the axis of rotation.

   Example:

   Suppose that we revolve the 4x4 frame with width 1 centered about (6,2) about the y-axis.  Then we have that the Area is

   A = 4 + 4 + 2 + 2 = 12

   R = 7 so that

   V = 2p7(12) = 168p

   Exercise:  Find the volume of the torus formed by revolving the disk

   (x - 11)² + y² = 4 

   about the y-axis.