The Volume of Cored Sphere

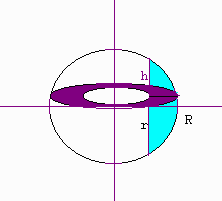
Let S be a sphere of radius R, center at the origin and let C be a cylinder of radius r (r < R) with the z-axis the axis of rotation.  We are concerned with the volume of the part of S outside C.  This cored sphere can also be realized by taking the region bounded by the circle         

        x² + y² = R²  

and the line 

        x = r 

and revolving it around the y-axis.  Taking a cross-section perpendicular to the y-axis and revolving it around the y-axis produces a washer.  The inner radius of the washer is r and the square of the outer radius of the washer is 

        R² - y²

Let h be the the height of the region (from the x-axis). 

        h = R² - r²

 Hence the area of the washer is

        Area =  p[(R² - y² ) - r²] = p[(R² - r² ) - y²] = p[h² - y²]

The smallest y value the cross-section will have is -h and the largest is h.

We can write this as an integral

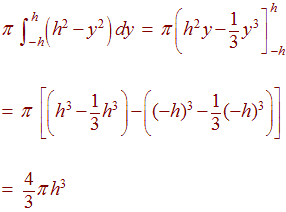
Notice that the volume only depends on the height of the region.