Cylindrical Shells

 

Cylindrical Shells


       

Consider rotating the region between the curve 

        y = x2
the line 

        x = 2 
and the x-axis about the y-axis.  

If instead of taking a cross section perpendicular to the y-axis, we take a cross section perpendicular to the x-axis, and revolve it about the y-axis, we get a cylinder.  Recall that the area of a cylinder is given by:


A = 2p r h

 

where r is the radius of the cylinder and h is the height of the cylinder.  We can see that the radius is the x coordinate of the point on the curve, and the height is the y coordinate of the curve.  Hence 

        A(x) = 2pxy = 2px(x2)

Therefore the volume is given by

       

 

Example:   

Find the volume of revolution of the region bounded by the curves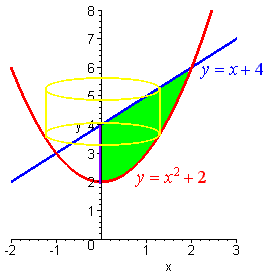 

        y = x2 + 2,      y =  x + 4,    and the y-axis
about the y axis.

Solution:

We draw the picture with a cross section perpendicular to the x-axis.  The radius of the cylinder is x and the height is the difference of the y coordinates:  

        h = (x + 4) - (x2 + 2)

We solve for b.  

        (x + 4) = (x2 + 2)
        x2 - x - 2 = 0 

        (x - 2)(x + 1) = 0
So that b = 2.  Hence the volume is equal to

       


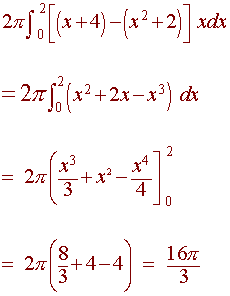
Exercises

Find the volume of the solid formed by revolving the given region about the given line

  1. y = x2 - 3x + 2, y = 0 about the y-axis

  2.  y = x2 - 7x + 6, y = 0 about the y-axis

  3. x = 1 - y2 , x = 0 (first quadrant) about the x-axis

  4. y = xsqrt(1 + x3), y = 0, x = 2 about the y-axis

  5. (x - 1)2  + y2  = 1 about the y-axis

  6. x2  + (y - 1)2  = 1 about the x-axis

  7. y  =  x2 - 2x + 1, y = 1 about the line x  =  3

  Answers

Back to Area and Volume Page

Back to Math 106 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions