The Second Derivative Test

I.  Quiz

II.  Homework

III.  Concavity and inflection Points

Example:  Consider a typical ski slope.  At what point on the slope are you having the most fun?  In other words where is the slope the greatest?  

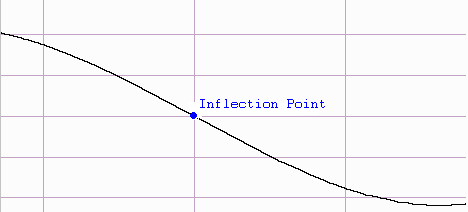
Definition:  If f'(x) is increasing then the function is concave up and if f'(x) is decreasing then the function is concave down.  To determine whether the derivative is increasing, we take the second derivative.  

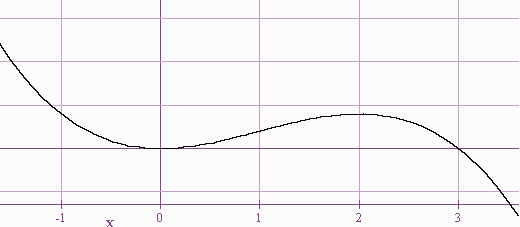
Example:  Let f(x) = 3x² - x³

Then  f'(x) = 6x - 3x² and f''(x) = 6 - 6x.  

Solving 6- 6x > 0, we see that the function is concave up when x <1

Solving 6- 6x <0, we see that the function is concave down when x > 1

When x = 1 we say that f(x) has an inflection point.  

Exercise:  Determine where the function is concave up and concave down:

A)  x³ - x

B)  x⁴ - 6x²

C)  x sqrt(x + 1)

IV.  The Second Derivative Test

We will see that at a relative maximum the curve is concave down, and for a relative minimum, the curve is concave up.  Hence we have:

Theorem:  The Second Derivative Test

Let f be a twice differentiable function near c such that f'(c) = 0.  Then

1)  If f''(x) > 0 then f(c) is a relative minimum

2)  If f''(x) < 0 then f(c) is a relative maximum

3)  If f''(x) = 0 then use the first derivative test.

Example:

Let f(x) = x⁴ - 4x³

Then f'(x) =  4x³ - 12x²   which is zero at x = 0 and x = 3

f''(x) = 12x² - 24x

f''(0) = 0 and f''(3) > 0

Hence at x = 3 there is a relative minimum.  At x = 0 we use the first derivative test.  To the left of 0 f'(x) < 0 and to the right of 0 f'(x) <0 thus at x = 0 there is no local extrema.

Exercises:  

f(x) = 5 + 3x² - x³    

f(x)  =  x⁴ - 4x³ + 2

f(x) =   x + 4/x