Graphing Rational Functions

I.  Quiz

II.  Homework

III.  Curve Sketching

List of interesting parts of a graph

A) x-intercepts

B) y-intercepts

C) Domain and Range

D) Continuity

E) Vertical Asymptotes

F) Differentiability

G) Intervals of Increase and Decrease

H) Relative Extrema

I) Concavity

J) Inflection Points

K) Horizontal Asymptotes

Example:  

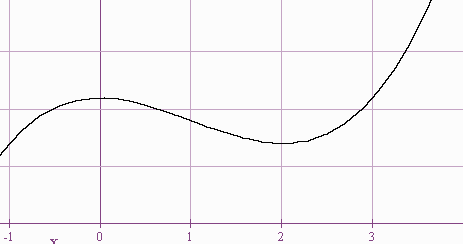
Graph x³ - 3x² -9x

1.  We find the x intercepts by factoring out the x and putting into the quadratic formula.

(-1.8,0), (0,0), (4.9,0).

2.  Note that the y intercept is also (0,0).

3.  The domain is R since this is a polynomial.

4.  The function is continuous since it is a polynomial.

5.  There are no vertical asymptotes since we have a polynomial.

6.  The function is differentiable everywhere.

7.  We find f'(x) = 3x² - 6x - 9 = 3(x - 3)(x + 1).

We see that f is increasing on (-infinity,-1) and on (3,infinity).  f is decreasing on (-1,3)

8. By the first derivative test, f has a relative maximum at (-1,5) and a relative minimum at (3,-27)

9.  f''(x) = 6x - 6, so that f is concave down on (-infinity,1) and concave up on (1,infinity)

10.  f(x) has an inflection point at (1,-11)

11.  f has no horizontal asymptotes.

The graph of f is shown below:

Example

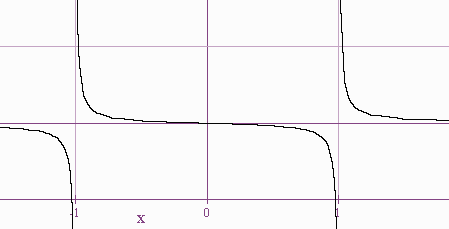
Graph x /(x² - 1)

x-int at (0,0)

Same for y-int

f'(x) = ((x² - 1)(1) - x(2x))/(x² - 1)² = (-x² - 1)/(x² - 1)²

f'(x) = 0 never, so there are no local extrema

and f(x) is increasing when x > 1 or x < -1

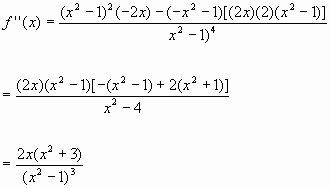
is 0 when x = 0 is positive when x is between - 1 and 0 or x is greater than 1. This is where f(x) is concave up. It is concave down elsewhere except at 0 and +-1.

F(x) has a vertical asymptote at x = 1 and -1.

The horizontal asymptote is y = 0.