The First Derivative Test

I.  Return Midterm II

II.  Homework

III.  The First Derivative Test

If f is a function, then f has a relative maximum at x = c if for all points a near c, f(c) > f(a), and f has a relative minimum at x = c if for all points a near c,  f(c) < f(a).

Consider a relative maximum, we have that on the left, the function is increasing and on the right the function is decreasing.  Similarly, for a relative minimum, on the right the function is decreasing and on the left the function is increasing.

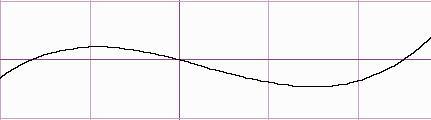
We can now state the first derivative test:

Let f'(c) = 0 then

1)  If f'(x) changes from positive to negative, then f has a relative maximum at c.

2)  If f'(x) changes from negative to positive, then f has a relative minimum at c.

Example:

Find and classify the relative extrema of

f(x) = x(1 - x)^2/5  

Solution

f'(x) = (1 - x)^2/5  -  2/5 x(1 - x)^-3/5  = 0 

Now multiply by (1 - x)^3/5

(1 - x) - 2/5 x = 0,  1 - 7/5 x = 0, x = 5/7 = 0.714

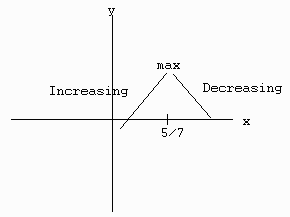
So there is a critical point at 5/7.  To determine whether the critical point is a relative max, min or neither, choose a number just above and just below the critical value.  

x	0.7	0.8
f'(x)	0.04	-0.3
Result	Increasing	Decreasing

So we see that f is increasing to the left of the critical number and decreasing to the right of the critical number.  Hence 5/7 is a relative maximum.

Exercise

A.  Classify the relative extrema of

 f(x)= x + 1/x

B.  An electric current in amps is given by

where w is a nonzero constant.   Find the maximum values of the current.