KEY TO PRACTICE MIDTERM II

Problem 1

  1. False, we need f(b) = f(a) for Rolle’s Theorem.
  2. True, f’(x) + g’(x) > 0 is both f’(x) and g’(x) are.
  3. False, try
, then 6 is not a critical point of fg.

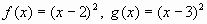
Problem 2

  1. No CP, No Inf. Pts, HA at y = 1, VA at x = -1.
  2. Rel max at (0,0), rel min at (2,-16) and (-2,-16), No asymptotes.

Problem 3

The distance function s(t) is continuous, since otherwise there would be a time warp. Since at some time, b, the ball must pass the hands’ height (IVT), s(0) = s(b), Rolle’s Theorem says that there is a c with s’(c) = 0, but s’ is the velocity function, so after c seconds the ball is not moving.

Problem 4

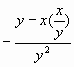
Problem 5

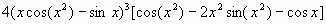
  2. (-sinx)(cos(cosx))(-sin(sin(cosx)))

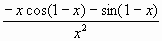
Problem 6

  1. 360 ft/sec
  2. 12/175 rad/sec