Inverse Trig and Hyperbolic Derivatives

I.  Return Midterm I

III.  Definition of the Inverse Trig Functions

Recall that we write arcsinx to mean the inverse sin of x restricted to have values between -pi/2 and pi/2 (Note that sin x does not pass the horizontal line test, hence we need to restrict the domain.)  We define the other five arctrig functions similarly.

III.  Trig of Arctrig Functions:

Example:  Find tan(acrsin(x))

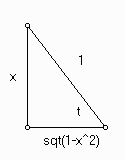
The triangle above demonstrates that

sin(t) = x/1 = opp/hyp.

Hence adj = sqrt(1 - x²) Since the tangent is opp/adj.  We have

tan(arcsin(x)) = x/sqrt(1 - x2)

Exercise

cos(arctan(2x))  

IV)  Derivatives of the Arctrig Functions

Recall that if f and g are inverses, then g'(x) = 1/f'(g(x))

What is d/dx(arctan(x))?

We use the formula:

1/sec²(arctan(x))  = cos²(arctan(x)).  

Since tan(theta) = opp/adj = x/1, we have hyp = sqrt(1 + x²) so that

cos²(arctan(x)) = [1/sqrt(1 + x²⁾] ²= 1/(1 + x²)

Theorem:

d/dx(arctan(x)) = 1/(1 + x2) d/dx(arcsinx) = 1/sqrt(1 - x2) d/dx(arcsecx) = 1/xsqrt(x2 - 1)

Recall that cosx = sin(pi/2 - x) hence arccosx = pi/2 - arcsinx

hence d/dx(arccosx) = d/dx[pi/2 - arcsinx] = -d/dx[arcsinx] = -1/sqrt(1 - x²)

Similarly:

d/dx(arccot(x)) = -1/(1 + x²)

d/dx(arccscx) = -1/xsqrt(x² - 1)

Example:

Find the derivative of cos(arcsinx)

Solution:  let y = cosu, u = arcsinx

y' = -sinu = -sin(arcsinx) = x

u' = 1/sqrt(1 - x²)

We arrive at

d/dx cos(arcsinx) = x/sqrt(1 - x²)