Derivative Theorems Part I
I. Quiz
II. Homework
III. Rolls Theorem
Let f(x) be differentiable on [a,b] with
f(a) = f(b)
then there is a c with f'(c) = 0
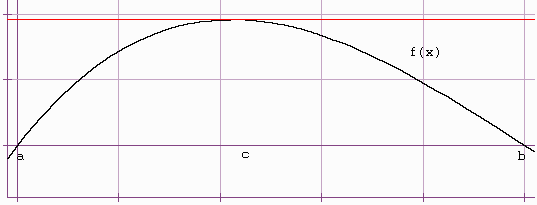
Proof: Since f(x) has a max and a min, one of the max or min must not be an endpoint. Hence f'(c) = 0 for some c.
IV. The Mean Value Theorem
Let f be a continuous function on [a,b] and differentiable on (a,b), then there exists a number c in (a,b) such that
f'(c) = (f(b) - f(a))/(b - a)
In other words there is a point c such that f'(c) = the slope of the secant from a to b.

Example: Suppose that at 10:00 you are spotted by a police officer near the Y, and that at 10:05 you are spotted in Myers (5 miles from the Y). The second officer claims that somewhere you must have been traveling exactly 60 miles per hour. Is the officer justified?
Solution: Let 10:00 correspond to t = 0 and the Y correspond to s = 0 then a = 0, b = 1/12, f(a) = 0 and f(b) = 5, so there is a c between and b (some time between 10:00 and 10:05) such that f'(c) = (5 - 0)/(1/12 - 0) = 60. Therefore the officer can give at ticket.
V. The Intermediate Value Theorem
If f is continuous on [a,b] and f(a) < k < f(b) then there exists at least one number c in the closed interval [a,b] for which f(c) = k
In particular if f(a) and f(b) have different signs, then f has a root between a and b.
VI. The Extreme Value Theorem
If f is continuous on [a,b] then
a) there is at least one number c in [a,b] such that f(c) is a global minimum.
b) there is at least one number d in [a,b] such that f(d) is a global maximum.