Key to the Practice Final

Problem 1

A.  True, A differentiable function is always continuous.

B.  False, if f(3) = f(4) then Roll's theorem would state that f'(c) = 0

C.  True, by the second fundamental theorem of calculus.

Problem 2

3tan(1 - x) + 3x[(-1)sec²(1 - x)] 

Problem 3

lim [(1 - 2(x + h)²) - (1 - 2x²)]/h  

= lim [1 - 2x² - 4xh - 2h²  - 1 + 2x²]/h = lim (-4xh -2h²)/h = lim -4x - 2h = -4x

Problem 4

lim xcsc(2x) = lim x/sin(2x) = lim[(u/2)/sin(u)] = 1/2 lim u/sinu = 1/2(1) = 1/2

Problem 5

A.  1/8

B.  x^3/3-2sqrtx-cosx + C

Problem 6

y' = 3x² - 12x - 15 = 3(x - 5)(x + 1)

y '' = 6x - 12

A.  Critical points are at (5,-60) and (-1,48)

since y''(5) > 0, (5,-60) is a  local minimum

since y''(-1) < 0,  (-1,48) is a local maximum

B.  Inc on (-infinity,-1) and (5,infinity), Dec on (-1,5)

C.  Inflection point at (2,-6)

D.  Covcave up on (2,infinity), Concave down on (-infinity,2)

E.  NA

F.  NA

G.  Not shown here.

Problem 7

A.  -3 ft/sec²

B.  9.356 seconds

C.  28 ft/sec

Problem 8

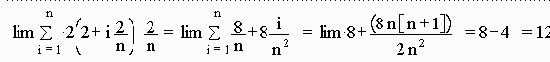
Problem 9

800 = xy, C = 2x + y

Hence y = 800/x so that C = 2x + 800/x

C' = 2 - 800/x² = 0 gives

x = 20 so that y = 800/20 = 40

Build the dock with dimensions 40 by 20.