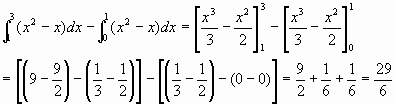The First Fundamental Theorem of Calculus
I. Quiz
II. Homework Questions
III. The First Fundamental Theorem of Calculus
Let f be a continuous function on [a,b] and let F'(x) = f(x) then
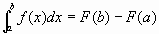
Proof: Cut up the interval [a,b] into several pieces with
a = x0 < x1 < x2 < x3 < ... < xn-1 < xn = b
Then
F(b) - F(a) = [F(xn) - F(xn-1)] + [F(xn-1) - F(xn-2)] + [F(xn-2) - F(xn-3)] +... + [F(x2) - F(x1)] + [F(x1) - F(x0)]
= ![]()
By the mean value theorem there is a ci between xi-1 and xi with
![]()
Clearing the denominator and substituting into the sum gives
![]()
Taking the limit as n approaches infinity, gives the definite integral.
Example:
![]()
We will try many others.
Example:
Find the area bounded by the curve y = x2 - x , y = 0, x = 4
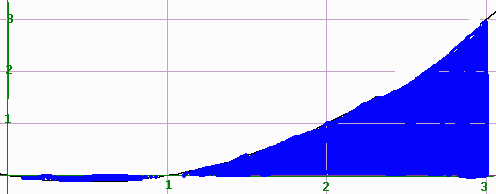
Notice that there is area both below the x-axis and above. We can find: