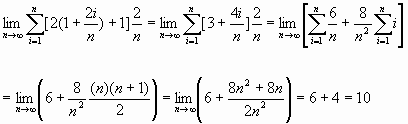Area
I. Homework
II. Area of a rectangle and using rectangles to approximate area under a curve
Recall that the area of a rectangle is the height times the base. What if we wanted to paint a wall that has a ceiling the shape of y = x2 , a flat floor and a right wall at x = 2 yards and a left wall at x = 5 yards.
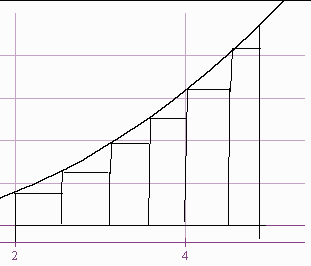
We can approximate the area by cutting out 6 rectangles. Since the base of the wall is 5 - 2 yards long, and there are 6 rectangles, the base of each rectangle is (5 - 2)/6 = .5 yards. The height of each rectangle is the y-coordinate of the left side of each rectangle. The x- coordinates are
2 + 0(.5),2 + 1(.5), 2 + 2(.5), 2 + 3(.5), 2 + 4(.5), 2 + 5(.5) so that the y coordinates are
(2 + 0(.5))2,(2 + 1(.5))2, (2 + 2(.5))2, (2 + 3(.5))2, (2 + 4(.5))2, (2 + 5(.5))2
We see that the ith rectangle has y coordinate:
height = (2 + i(.5))2 = 4 + 2i + .25i2
To get the area of the ith rectangle we multiply the height by the base:
(4 + 2i + .25i2)(.5)
Finally to get the total area we add the terms up:
sum[(4 + 2i + .25i2)(.5)]
This will be a lower bound for the area.
Exercise: Find an upper bound for the area.
III. Left and Right Sums
If we take the limit as i approaches infinity, We arrive at the formulae:
Left Sum
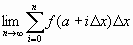
Right Sum
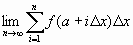
Note: f(x) can be negative
Usually to compute a definite integral, we use left or right sums.
Example
Use the right sum to find ![]()
Solution: The right sum is