Derivative Theorems

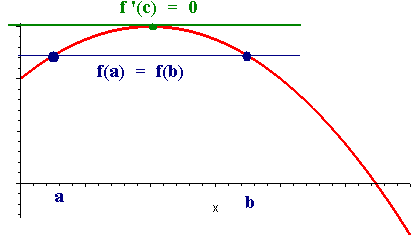
Rolle's Theorem

 Rolle's theorem says that if a ball is thrown up and comes back down,  then at some time along its journey it is neither going up or down, i.e., it reaches a maximum.  Formally it says...

Rolle's Theorem

Let f(x) be differentiable on [a,b] with

          f(a) = f(b) 

then there is a c with f '(c) = 0

 



       


Proof:  

Since f(x) has a max and a min, one of the max or min must not be an endpoint.
Hence 

        f '(c) = 0 for some c.

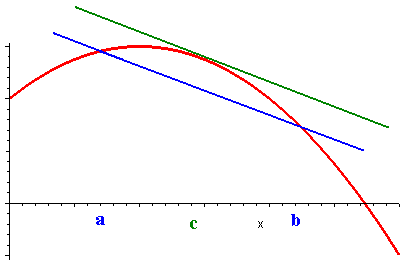
The Mean Value Theorem

The mean value theorem states that the instantaneous velocity equals the average velocity somewhere along the trip.  


The Mean Value Theorem

Let f be a continuous function on [a,b] and differentiable on (a,b), then there exists a number c in (a,b) such that

                         f(b) - f(a)
         f '(c)  =                        
                            b - a

 


In other words there is a point c such that f '(c) equals the slope of the secant from a to b.  

       



Example:  

Suppose that at 10:00 you are spotted by a police officer near the Y, and that at 10:05 you are spotted in Myers (5 miles from the Y).  The second officer claims that somewhere you must have been traveling exactly 60 miles per hour.  Is the officer's claim justified?

Solution:  

Let 10:00 correspond to t = 0 and the Y correspond to s = 0 then a = 0, b = 1/12, f(a) = 0 and f(b) = 5, so there is a c between a and b (some time between 10:00 and 10:05) such that

                           5 - 0
        f '(c) =                       = 60 
                        1/12 - 0 

 Therefore the officer's claims are valid.  

 The Intermediate Value Theorem

The intermediate value theorem says that if you trace a continuous curve with your starting point f(a) units above the x-axis and your ending point f(b) units above the x-axis, then your pencil will draw points at all heights between f(a) and f(b).

The Intermediate Value Theorem

If f is continuous on [a,b]  and 

           f(a) < k < f(b) 
then there exists at least one number c in the closed interval [a,b] for which f(c) = k


Corollary If f(a) and f(b) have different signs, then f has a root between a and b.  


Example

Show that the polynomial 

        y = x7 - 2x6 + 3x4 + x3 - 4x - 10

Has a root on the interval [0,2]


Solution

We have 

        y(0) = -10

and

        y(2) = 38

since

        -10 < 0 < 38

and since y(x) is a polynomial, in particular continuous, the intermediate value theorem tells us that y(c) = 0 for some value of c between 0 and 2.

The Extreme Value Theorem

The extreme value theorem tell us that all continuous function reach a top and a bottom.

The Extreme Value Theorem

If f is continuous on [a,b] then

  1. There is at least one number c in [a,b] such that f(c) is a global minimum.

  2. There is at least one number d in [a,b] such that f(d) is a global maximum.

 

Back to Math 105 Home Page

e-mail Questions and Suggestions