The Product and Quotient Rules

The Product Rule

Theorem  (The Product Rule) Let f and g be differentiable functions.  Then           [f(x) g(x)] ' = f(x) g '(x) + f '(x) g(x)

Proof:

We have 

       

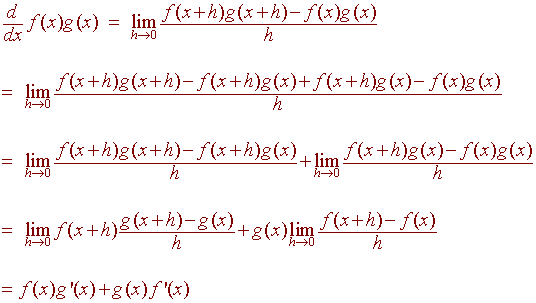
Example

Find

        d
               (2 - x²)(x⁴ - 5)
        dx

Solution:    

Here

        f(x)  =  2 - x² 

and

        g(x)  =  x⁴ - 5

The product rule gives

          d
               (2 - x²)(x⁴ - 5)  =  (2 - x²)(4x³) + (-2x)(x⁴ - 5)
        dx

The Quotient Rule

Remember the poem

        "lo d hi minus hi d lo square the bottom and away you go"

This poem is the mnemonic for the taking the derivative of a quotient.

Theorem:           d    f             g f '  -  f g '                       =                                      dx   g                  g2

Example:

Find y' if

                   2x - 1
        y'  =                
                    x + 1

Solution:

Here

        f(x) = 2x - 1

and

        g(x) = x + 1

The quotient rule gives

                (x + 1)(2) - (2x - 1)(1)
                                                       
                          (x + 1)² 

                    2x + 2 - 2x + 1
        =                                      
                        (x + 1)² 

                         3
        =                               
                    (x + 1)² 

Other Derivative Sites

Visual Calculus

Karl's Calculus

CyberCalc Derivatives

Eric Weisstein's Calculus

Dr. Sloan's Calculus

Product Rule Problems and Solutions

Quotient Rule Problems and Solutions

Product Rule by Harvey Mudd

Quotient Rule by Harvey Mudd

Back to Math 105 Home Page

e-mail Questions and Suggestions