Derivatives The Easy Way

 Constant Rule and Power Rule

We have seen the following derivatives:

1. If f(x) = c, then f '(x) = 0
   

2. If f(x) = x, then f '(x) = 1
   

3. If f(x) = x², then f '(x) = 2x
   

4. If f(x) = x³, then f '(x) = 3x²
   

5. If f(x) = x⁴, then f '(x) = 4x³
   

This leads us the guess the following theorem.

Theorem       d             xn  =  nxn-1      dx

Proof:

We have

       

Applications

Example

Find the derivatives of the following functions:

1. f(x) = 4x³ - 2x¹⁰⁰
   

2. f(x) = 3x⁵ + 4x⁸ - x + 2
   

3.  f(x) = (x³ - 2)²
   

Solution  

We use our new derivative rules to find

1. 12x² - 200x⁹⁹
   

2. 15x³+32x⁷-1
   

3. First we FOIL to get
   
           [x⁶ - 4x³ + 4] ' 
   
   Now use the derivative rule for powers
   
           6x⁵ - 12x² 
   

Example:

Find the equation to the tangent line to 

        y  =  3x³ - x + 4 

at the point (1,6)

Solution:

        y'  =  9x² - 1 

at x = 1 this is 8. Using the point-slope equation for the line gives

        y - 6  =  8(x - 1) 

or 

        y  =  8x - 2

Example:

Find the points where the tangent line to 

        y  =  x³ - 3x² - 24x + 3 

is horizontal.

Solution:

We find 

        y'  =  3x² - 6x - 24

The tangent line will be horizontal when its slope is zero, that is, the derivative is zero.  Setting the derivative equal to zero gives:

        3x² - 6x - 24  =  0 

or

        x² - 2x - 8  =  0 

or

        (x - 4)(x + 2)  =  0

so that 

        x = 4    or    x = -2

Derivative of f(x) = sin(x)

Theorem       d             sin(x)  =  cos(x)      dx

Proof:  

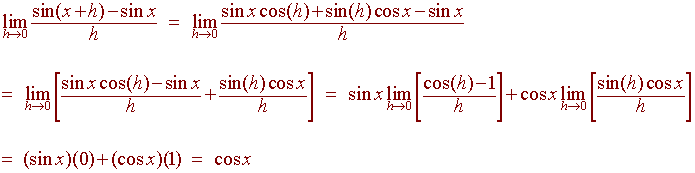
d/dx cos(x)

 

Theorem        d                 cos x  =  -sin x       dx

Back to Math 105 Home Page

e-mail Questions and Suggestions