Graphing Rational Functions

A List of Interesting features of a Graph

Below is a list of features of a graph that may assist in curve sketching:

1. x-intercepts
   

2. y-intercepts
   

3. Domain and Range
   

4. Continuity
   

5. Vertical Asymptotes
   

6. Differentiability
   

7. Intervals of Increase and Decrease
   

8. Relative Extrema
   

9. Concavity
   

10. Inflection Points
    

11. Horizontal Asymptotes
    

Most graphs contain only some of these eleven features, so to sketch a graph we find as many interesting features as possible and use these features to sketch the graph.

Examples

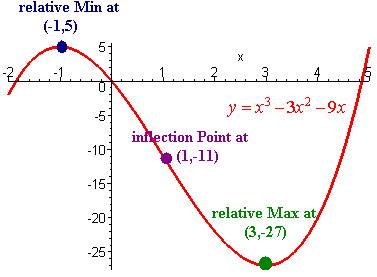
Example 1

Graph 

y = x³ - 3x² - 9x

1. We find the x intercepts by factoring out the x and putting into the quadratic formula.
   
           (-1.8,0), (0,0), (4.9,0).
   

2. Note that the y intercept is also (0,0).
   

3. The domain is R (all real numbers) since this is a polynomial.
   

4. The function is continuous since it is a polynomial.
   

5. There are no vertical asymptotes since we have a polynomial.
   

6. The function is differentiable everywhere.
   

7. We find 
   
           f '(x) = 3x² - 6x - 9 = 3(x - 3)(x + 1).
   
   We see that f is increasing on (-,-1) and on (3,).  f is decreasing on (-1,3).
   

8. By the first derivative test, f has a relative maximum at (-1,5) and a relative minimum at (3,-27).
   

9.         f ''(x) = 6x - 6 
   
   so that f is concave down on (-,1) and concave up on (1,).
   

10. f(x) has an inflection point at (1,-11).
    

11. f has no horizontal asymptotes.

The graph of f is shown below:

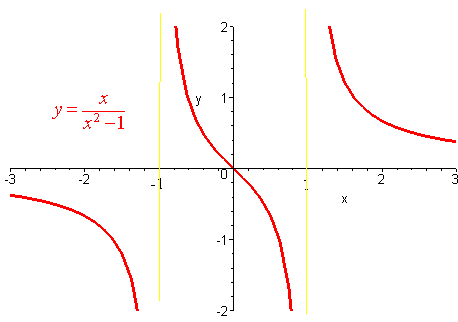
Example 2

Graph 

                     x
      y =                     
                  x² - 1

Solution:

The x-intercept is at (0,0)

Same for the y-int

                        (x² - 1)(1) - x(2x)                -x² - 1
        f '(x) =                                         =                      
                                (x² - 1)²                       (x² - 1)²

f '(x)  =  0 has no solution since the numerator is always negative, so there are no local extrema. Since the denominator is always nonnegative,  f(x) is decreasing for all x not equal to -1 or 1 where the function is undefined.

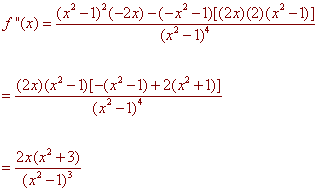
                        (x² - 1)²(-2x) - (-x² - 1)[(2x)(2)(x² - 1)]
        f ''(x)  =                                                                        
                                            (x² - 1)⁴

                    (2x)(x² - 1)[-(x² - 1) + 2(x² + 1)]
        =                                                                    
                                     (x² - 1)⁴ 

                        2x(x² + 3)
        =                                        
                          (x² - 1)³ 

is 0 when x = 0 and is positive when x is between - 1 and 0 or x is greater than 1. This is where f(x) is concave up. It is concave down elsewhere except at 0 and 1.

f(x) has a vertical asymptote at x = 1 and -1.

The horizontal asymptote is y = 0.

The graph is shown below.

Back to Math 105 Home Page

e-mail Questions and Suggestions