Newton's Method

Newton's Method


Consider finding the root of

        y = e^x - 4x

Try as you may, there is no algebraic technique that finds this root.  We will approximate the solution as follows:

The graph shows that a solution lies between 0 and 2.

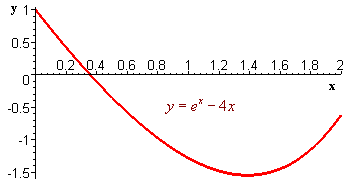
Our initial guess is 

        x = 1  

Now draw a tangent line through (1,f(1)).  Next see where the tangent line crosses the x-axis.  The tangent line is a close approximation to the curve for nearby values, hence the x-intercept of the tangent line is close to the x-intercept of the curve.  The tangent line has equation

        y - f(1) = f '(1)(x - 1)

The x intercept occurs when y = 0, hence

        -f(1) = f '(1)(x - 1)

solving for x,

                         f(1)
        x = 1 -                     
                        f '(1)

This x will not be the true root, but will be a better guess than x = 1.  We will use this (call it x₂)  as our second guess. Next play the same game:

                          f(x₂)
        x₃ = x₂ -                     
                         f '(x₂)

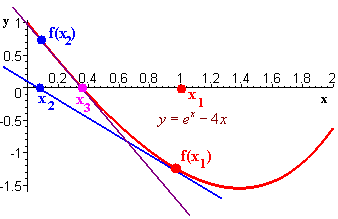
The graph below shows this construction.  The blue line is the first tangent line and the purple line is the second tangent line.

Continue this process to get

f(xn) xn+1 = xn -                                   f '(xn)

For our example this expression is

        

Use a calculator or computer to find the values.

        x₁ = 1,     x₂ = 0,     x₃ =.3333,     x₄ = .3572,     x₅ =.3574,     x₆ = .3574

We see that .3574 is the root accurate to 4 decimal places.  

Exercise

Estimate 

 using Newton's method.  
Hint:  Find the root of x² - 5.

When Newton's Method Fails

1. If our first guess  (or any guesses thereafter) is a point at which there is a horizontal tangent line, then this line will never hit the x-axis, and Newton's Method will fail to locate a root.  If there is a horizontal tangent line then the derivative is zero, and we cannot divide by f '(x) as the formula requires.
   

2. If our guesses oscillate back and forth then Newton's method will not work.
   

3.  If there are two roots, we must have a first guess near the root that we are interested in, otherwise Newton's method will find the wrong root.
   

4. If there are no roots, then Newton's method will fail to find it.  (This can be frustrating when you are using your calculator to find a root.  

Example

Explain why Newton's method fails to find the root of 

        f(x)  =  x^1/3 

with an initial guess of x  =  1.

Solution

We have

        f '(x)  =  1/3 x ^-2/3 

so that 

                                 x_n^1/3
        x_n+1 = x_n -                          =  x_n - 3x_n  =  -2x_n  
                             1/3 x ^-2/3 

This gives us

        x₁  =  1,        x₂  =  -2(1)  =  -2

        x₃  =  -2(-2)  =  4,        x₄  =  -2(4)  =  -8

These numbers are growing (in absolute value) instead of converging.  In fact, we have

        x_n  =  (-1)ⁿ 2^n-1 

Hence Newton's method fails.  However, it is clear that there is a root at x = 0.  Notice that at x = 0, the derivative is undefined.

An app to explore Newton's Method

A proof that Newton's Method will always converge for a cubic with a positive derivative.

Back to Math 105 Home Page

e-mail Questions and Suggestions