Composition and Inverses

I.  Homework

II.  Composition of Functions

Example:  Sociologists in Holland determine that the number of people waiting in a water ride at an amusement park is given by

y = 1/50C²  + C + 2

where C is the temperature in degrees C.  We have

C = 5/9 F + 160/9

To get a function of F we compose the two function:

y(C(F)) = (1/50)[5/9F + 160/9]² + (5/9F + 160/9) + 2

Exercises: 

 If f(x) = 3x + 2 , g(x) = 2x² + 1, h(x) = sqrt(x - 2), c(x) = 4

A)  Find f(g(x))

B)  Find f(h(x))

C)  Find f(f(x))

D)  Find h(c(x))

E)c(f(g(h(x))))

III.  1-1 Functions

A function f(x) is 1-1 if f(x) = f(b) implies that a = b

Example:  If f(x) = 3x + 1 then 3a + 1 = 3b + 1 implies that 3a = 3b

hence a = b therefore f(x) is 1-1.

Example:  If f(x) = x²  then a² = b²  implies that a² - b²  = 0 or that (a - b)(a + b) = 0 hence

a = b or a = -b.  For example f(2) = f(-2) = 4.  Hence f(x) is not 1-1.

IV.  Horizontal Line Test

If every horizontal line passes through f(x) at most once then f(x) is 1-1.

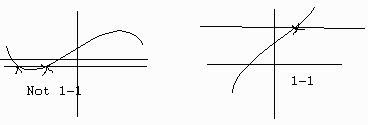
V.  Inverse Functions

Definition:  A function g(x) is an inverse of f(x) if

f(g(x)) = g(f(x)) = x

Example:  The volume of a lake is modeled by the equation

V(t) = 1/125 h³

 Show that the inverse is

h(N) = 5V^1/3  

We have h(V(h)) = 5(1/125h³)^1/3 = 5/5h = h

and v(h(V)) = 1/125(5V^1/3)³ = 1/125(125V) = V

VI)  Step by Step Process for Finding the Inverse:

1)  Interchange the variables

2)  Solve for y

3)  Write in terms of f^-1(x)

Example:

f(x) = y = 3x³ - 5

1)  x =  3y³ - 5

2)  x - 5 =  3y³ , (x - 5)/3 =  y³ , [(x - 5)/3]^1/3 

3)  f^-1(x) =  [(x - 5)/3]^1/3 

VII)  Graphing:  

To graph an inverse we draw the y = x line and reflect the graph across this line.

This will be demonstrated in class.