MAT 103A Practice Exam 1

Problem 1:  Determine if the triangle with vertices (3,-5), (2,4), and (1,1) is isosceles, equilateral, or neither.

Solution

A triangle is isosceles if two of its side lengths are equal and it is equilateral if all three are equal.  We find the lengths of the three sides.  The length of the side from (3,-5) to (2,4) is

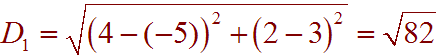
The length of the side from (3,-5) to (1,1) is

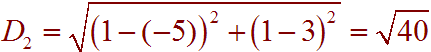
The length of the side from (2,4) to (1,1) is

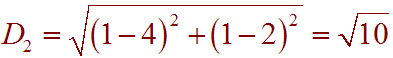
Since none of these side lengths are equal, the triangle is neither isosceles nor equilateral.

Problem 2:  Determine if the following are true or false.  Explain why your answer is correct.

A.  If (2,3) is a point on the graph of the function y = f(x) that is symmetric with respect to the y-axis, then (-2,-3) is also on the graph of y = f(x).

Solution

False, symmetry with respect to the y-axis gives that the point (-2,3) is on the graph of the function.

B.  Let the slope of line r be 3/2 and the slope of line s be -2/3.  If P is is the point of intersection of the two lines and if Q and R are points on lines r and s that are distinct from point Q, then the triangle with vertices P, Q, and R is a right triangle.

Solution

True, since the slopes are negative reciprocal's of each other, the lines are perpendicular.  Thus the angle QPR is a right angle.

C.  If f(x) = x² + 3x - k and if f(1) = 5, then f(2) = 9.

Solution

We have

f(1) = 5 = 1² + 3(1) - k

so that k = -1.  thus

f(2) = 2² + 3(2) + -1

so the statement is false.

D.  A circle is never the graph of a function of y in terms of x.

Solution

This is true since a circle does not pass the vertical line test.

E.  If f(x) is an increasing function between 3 and 7 and if f(4) = 0 then f(5) cannot be negative.

Solution

This is true, since if f(5) was negative, then f(5) < f(4) which contradicts that fact that f(x) is increasing.

Problem 3:  List the intercepts and test for symmetry.  4x² + 9y² = 36

Solution

To find the x-intercepts, plug in y = 0:

4x² + 0 = 36

Solving gives the x-intercepts of (-3,0) and (3,0).

To find the y-intercepts plug in x = 0:

0 + 9x² = 36

Solving gives the y-intercepts of (0,-2) and (0,2).

If we plug in -x for x we get

4(-x)² + 9y² = 36

This is equivalent to

4x² + 9y² = 36

Thus the function is symmetric with respect to the y-axis.

If we plug in -y for y we get

4x² + 9(-y)² = 36

This is also equivalent to

4x² + 9y² = 36

Thus the function is symmetric with respect to the x-axis.

If we plug in -x for x and -y for y we get

4(-x)² + 9(-y)² = 36

This is also equivalent to

4x² + 9y² = 36

Thus the function is symmetric with respect to the origin.

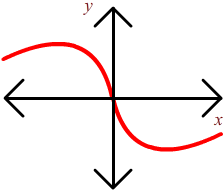
Problem 4:  The sketch below shows part of the function y = f(x) that is symmetric with respect to the origin.  Sketch the rest of the function.

Solution

A graph that is symmetric with respect to the origin had the property that if a piece is reflected about the x-axis and then the y axis then the image is still part of the graph.  First reflect across the x-axis to get:

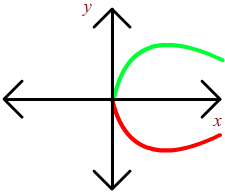
Now reflect across the y-axis to get the final graph:

Problem 5:  Use a calculator to sketch the graph of y = x³ - 4x² + x + 2.  Then approximate the intercepts, the relative maximum and minimum, and where the function is increasing and where it is decreasing.

Solution

The graph is shown below:

The y-intercept is at (0,2), the x-intercepts are at (1,0) and approximately at (-0.56,0) and (3.56,0).  The relative maximum is at approximately (0.13,2.06) and the relative minimum is approximately at (2.54,4.88).  The function is increasing from negative infinity to 0.13 and from 2.54 to infinity.  The function is decreasing on the interval (0.13,2.54).

Problem 6:  A waiter receives $8 an hour in base wages plus 15% of all receipts from the tables that he serves.  Write a linear model that relates the waiter's hourly wage W when his total receipts is R dollars.

Solution

If the waiter has 0 receipts, his hourly wage is $8, thus the y-intercept is at (0,8).  The slope is 0.15, since a $1 increase in R gives a $0.15 increase in W.  Thus the linear model has equation

W = 0.15R + 8

Problem 7:  Find the center and radius of the circle x² + y² - 10x + 4y  =  7.  Then graph the circle.

Solution

We first have to complete the squares.  Reorder the terms to get

x² - 10x + y² + 4y  =  7

Next add the "magic numbers" by squaring b/2.  The first magic number is (-10/2)² = 25 and the second magic number is (4/2)² = 4.

x² - 10x + 25 + y² + 4y + 4  =  7 + 25 + 4

Now factor and perform the arithmetic on the right hand side

(x - 5)² + (y + 2)² =  36

Thus the center is at (5,-2) and the radius is 6.  The graph is shown below.

Problem 8:  Find the equation of the circle that has diameter with endpoints (-1,2) and (3,-1).

Solution

We need to find the center and the radius for this circle.  Since the points are the endpoints of the diameter, the center will be the midpoint of the two points.  We have

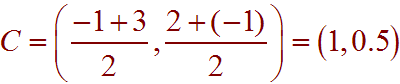
The radius is half the distance between the two endpoints of the diameter.  We have

The equation of the circle is

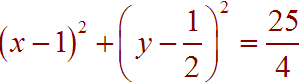
Problem 9:  Find the domain of the function

Solution

The domain of a function is all the values of x that can be plugged in so that we get a value for y.  The issue is that there is a denominator and there is a square root.  The inside of a square root has to be nonnegative and the denominator cannot be 0.  Hence the inside of the square root must be positive.  We have

1 - x  >  0

or

x < 1

In set notation the domain is

Domain = {x | x < 1}

Problem 10:  If a ball is dropped from a building its height h off the ground in feet after t seconds is h(t) = -16t² + 320.  When will the ball hit the ground?

Solution

The ground corresponds to a height h of 0.  We just set the equation equal to 0 and solve.

-16t² + 320  =  0

subtract 320 from both sides and then divide both sides by -16 to get

t²  =  20

Take a square root of both sides and note that the time must be positive to get that t is approximately equal to 4.47 seconds.

Problem 11:  Find the domain and range of the function shown below.  List any intercepts, symmetry with respect to the x-axis, y-axis, or the origin, any relative maximum and minimum, and the intervals where the function is increasing and where it is decreasing.

Solution

The domain is the values that x can take.  The farthest left the graph gets is about -2.5 and the farthest right it gets is about 2.  Thus the domain is (-2.5,2).  The range is the values that y takes on.  The lowest that the graph gets is about -3.5 and the highest is about 5.5.  Hence the range is (-3.5,5.5).  The y-intercept is at (0,2) and the x-intercepts are at (-2,0), (0.6,0), (1,0), and (1.6,0).  The relative maximum is at (0.1,2.1) and the relative minimum occurs at the points (-1.3,-3.4) and (1.3,0.6).  The function is increasing on (-1.3,0.1) and (1.3,2).  The function is decreasing on (-2.5,-1.3) and (0.1,1.3).

Problem 12:  Find the average rate of change of the function f(x)  =  x³ - 2x + 3 from -1 to 2.

Solution

We find

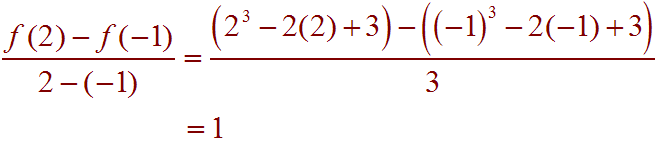
The average rate of change is 1.