LHopital's Rule

1. Proof of L'Hopital's Rule
   
   Goal:  Easily find lim as x -> 0 of (sinx)/x
   
   Suppose that f and g are continuous functions and f(a) = g(a) = 0
   Recall the mean value theorem states that

   f'(c) = (f(b) - f(a))/(b - a)

   so that

   f'(c)/g'(c) = (f(b) - f(a))/(g(b) - g(a))

   Let a = 0:

   Then f'(c)/g'(c) = (f(b) - f(0))/(g(b) - g(0)) = (f(b) -  0 )/(g(b) - 0) = f(b)/g(b)

   so that

   lim b -> 0 f(b)/g(b) = lim c -> 0 f'(c)/g'(c).

   Hence lim x -> 0 (sinx)/x = lim x-> 0 (cosx)/1 = 1.
   

   L'Hopital's Rule:  Let f(c) = g(c) = 0, then lim x-> c f(x)/g(x) = lim x -> 0 f'(x)/g'(x).

   Example:

    lim x -> 0 (e^x - 1)/x = lim x -> 0 e^x/1 = 1

   Exercises:

   A)  lim x -> 1 lnx/(x² - 1)

   B)  lim x-> 0 sinx/(x + 1)

   C)  lim x -> infinity e^-x/x²

   
   

2. Hidden Forms of L'Hopital's Rule
   We can also use L'Hopital's rule when we have expressions of the form (0)(infinity), (infinity)⁰, and infinity - infinity

   Example:  (0)(infinity) 

   

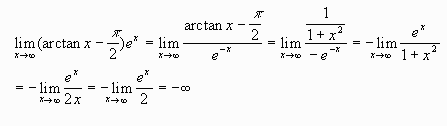
   Example:  (infinity)⁰

   

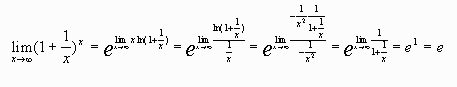
   Example:  infinity - infinity 

   lim x -> 1⁺ (1/(x² - 1) - 1/lnx)  = lim x -> 1⁺  [lnx - (x² - 1)]/[(x² - 1)lnx]

   = lim x -> 1⁺ [1/x - 2x]/[2xlnx + (x - 1)/x) = (1 - 2)/0 which is undefined.

   Exercise:  lim x -> 0⁺ x^x