Improper Integrals

1. Definition of Improper Integrals.

   If f(x) is continuous on (a,b] and not continuous at x = a, then we define
   

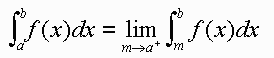
   Example:

   

    

2. Improper Integrals Involving Infinity:

   We define
   

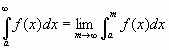
   Example:

   int from 1 to infinity of 1/x²  dx  =  lim as m -> infinity of int from a to m of 1/x² dx

   =  lim as m -> infinity of  -1/x from 1 to infinity =  lim as m -> infinity of  -1/m - (-1/1) = 0 + 1 = 1

   Exercises:  

   A) int from 0 to infinity of xe^-x dx

   B)  int from  -infinity to infinity of 1/(1 + x²) dx 

   C)  int from 0 to infinity of sinx dx

   D)  Determine for which values of p the integral

   int from 1 to infinity of 1/x^p dx converges.

   E)  Use the formula for arclength to show that the circumference of the semi-circle y = sqrt(r² - x²) is (pi)(r).