Name
MATH 105 PRACTICE EXAM 1
Please work out each of the given
problems. Credit will be based on
the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Please answer the following true or false. If false, explain why or provide a counter example. If true, explain why.
A) (7 Points) If f(x) and g(x) are differentiable functions with
f '(5)
= 10 and g'(5)
= 4
then if
f(x)
h(x) =
- 3g(x)
2
then
h'(5) = -7
B)
(7 Points) Let
f(x)
and
g(x)
be continuous functions
f(1) > g(1)
and
f(2) < g(2)
then if
h(x) = f(x) - g(x)
h(x)
has a root for some value of x
between 1 and 2.
C) (7 Points) Let f(x) and g(x) be continuous functions such that
![]() and
and
![]()
Then h(x) has a vertical asymptote at x = 2.
PROBLEM 2 Find the following limits if they exist:
A) (8 Points)
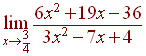
B) (8 Points)
![]()
C)
(8 Points)
![]()
PROBLEM 3
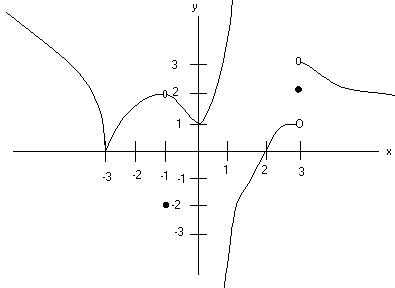
A) (8 Points) Find the following limits if they exist
i)
![]() ii)
ii)
![]() iii)
iii)
![]() iv)
iv)
![]() v)
v)
![]()
B) (8 Points) At which values is f(x) not continuous?
C) (8
Points) At which values is
f(x) not differentiable?
PROBLEM 4 (20 Points) Below is the function y = f(x). Sketch a graph of the derivative y = f ’(x).
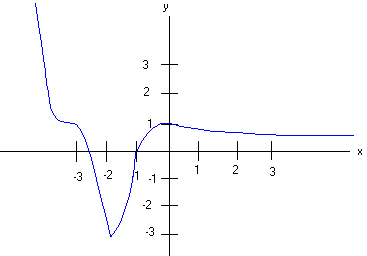
PROBLEM 5 Find f ' (x) for the following
A)
(10 Points)
![]()
B)
(11 Points)
![]()
PROBLEM 6 Let
![]()
A) (10 Points) Use the limit definition of the derivative to find f ’(x).
B)
(10 Points) Prove using the
e-d
definition of the
limit that
![]()
PROBLEM 7 (20
Points)
The position of a robin flying through the wind is given by
s(t) = -5t + tcost
Find its acceleration when t is 2 seconds.
Extra Credit: Write down one thing that your instructor can do to make the class better and one thing that you want to remain the same in the class.
(Any constructive remark will be worth full credit.)
Back to the Math Department Home
e-mail Questions and Suggestions