Review of Some Linear Algebra
In this discussion, we expect some familiarity with matrices. For a review of the basics click here. We will rely heavily on calculators and computers to work out the problems. Consider some examples.
Example
Solve the system of equations
4x + y +
3z = 2
x - 2y - 5z = 3
5x + 2z = 1
Solution
We write this system as the matrix equation
Ax = b
where
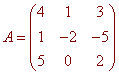
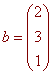
To solve this matrix equation we take the inverse of both sides (which is possible since the determinant of A is -13 which is not equal to zero. We have
x = A-1b
Using a calculator we find that
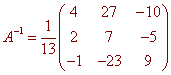
Multiplying by b gives
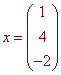
What we mean by "x" is the vector <x,y,z>. The solution is
x = 1 y = 4 z = -2
Example
Find the solution of
3x + 2y - z = 5
2x + y - z = 2
5x + 4y - z = 11
Solution
A quick check shows that we cannot solve this problem in the same way, since the determinant of A is 0. Instead, we rref the augmented matrix
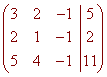
to get
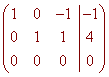
Putting this back into equation form, we get
x - z = -1 and y + z = 4
We write this as
x = -1 + z y = 4 - z z = z
Letting z = t be the parameter we get parametric equations for the solution set
x = -1 + t y = 4 - t z = t
Recall that vectors v1, ..., vn are called linearly independent if
c1v1 + ... + c2v2 = 0
implies that all of the constants ci are zero. A theorem from linear algebra tell us that if we have n vectors in Rn then they will be linearly independent if and only if the determinant of the matrix whose columns are these vectors has nonzero determinant.
Example
Show that the vectors
u = <1,4,-2> v = <0,3,5> and w = <1,2,3>
are linearly independent.
Solution
We find the determinant
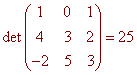
Since the determinant is nonzero, the vectors are linearly independent.
For systems of differential equations, eigenvalues and eigenvectors play a crucial role. We recall their definitions below
| Definition: Eigenvalues and
Eigenvectors
Let A be an n x n matrix. Then l is an eigenvalue for A with eigenvector v if Av = lv |
Example
Find the eigenvalues and eigenvectors for
![]()
Solution
If
Av = lv
then
A - lI = 0
Taking determinants of both sides, we get
(6 - l)(-1 - l) + 12 = 0
l2 - 5l + 6 = 0
(l - 2)(l - 3) = 0
The eigenvalues are
l = 2 and l = 3
To find the eigenvectors, we plug the eigenvalues into the equation
A - lI = 0
and find the null space of the left hand side. For the eigenvalue l = 2, we have
![]()
The first row gives
y = -x
so that an eigenvector corresponding to the eigenvalue l = 2 is
![]()
For the eigenvalue l = 3, we have
![]()
The first row gives
3y = -4x
so that an eigenvector corresponding to the eigenvalue l = 3 is
![]()
Typically, we want to normalize the eigenvectors, that is find unit eigenvectors. We get
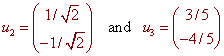
Back to the Power Series Methods and Laplace Transforms Home Page
Back to the Differential Equations Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions