Homogeneous Systems

The Null Space

We have seen that the solution to the homogeneous system of equations 

        Ax  =  0

is a subspace of Rⁿ.  We will now begin a discussion of how to find a basis for this system.  The approach we will take is by an illustrative example.

Example

Find a basis for the null space of the matrix

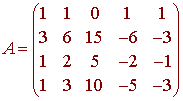
Solution

We have seen before that the null spaces of row equivalent matrices are the same.  Hence this question is equivalent to that of finding the null space of 

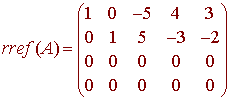
Now lets rewrite the system in equation form

        x₁       -5x₃ + 4x₄ + 3x₅  =  0
             x₂ + 5x₃ - 3x₄ - 2x₅  =  0

We can move the last three variable (the ones that are not corner variables) to the right hand side of the equations and add identity equations to get

        x₁  =  5x₃ - 4x₄ - 3x₅
        x₂  =  -5x₃ + 3x₄ + 2x₅
        x₃  =     x₃
        x₄  =     x₄
        x₅  =     x₅

It is useful to introduce parameters here

        s₁  =  x₃        s₂  =  x₄        s₃  =  x₅

so that

        x₁  =  5s₁ - 4s₂ - 3s₃
        x₂  =  -5s₁ + 3s₂ + 2s₃
        x₃  =     s₁
        x₄  =              s₂
        x₅  =                       s₃

and we can write this in vector form

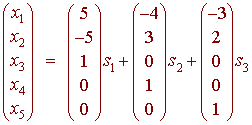
We can see that the null space is represented by triplets (s₁, s₂, s₃).  This is equivalent (isomorphic) to the space R³.  We select the standard basis 

        (1,0,0), (0,1,0), (0,0,1)

and come up with the basis for the null space

        {(5,-5,1,0,0), (-4,3,0,1,0), (-3,2,0,0,1)}

Example

Let 

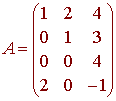
Find the null space of A.  

Solution

As before, we find rref the matrix.

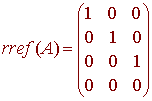
The corresponding equations are

        x₁  =  0
        x₂  =  0
        x₃  =  0

and we see that the null space is the subspace containing only 0. 

Nonhomogeneous Systems

Now that we know how to solve the homogeneous equation

        Ax  =  0

we move on to nonhomogeneous systems

        Ax  =  b

We use the technique of rref as with homogeneous systems.  The next example illustrates.

Example

Solve

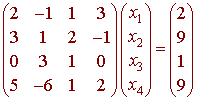
Solution

We solve the augmented matrix

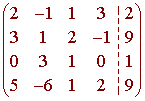
and find the rref of the augmented matrix.  We get

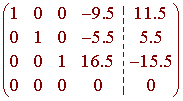
This gives us the solution

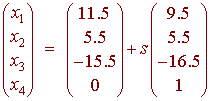
Notice that this is not a vector space (it does not contain the zero vector) so it does not make sense to ask for a basis for a null space.

The above answer shows that 

The solution to 

        Ax  =  b 

can be written in the form 

        x  =  x_p + x_h 

Where 

        x_p is a particular solution to the nonhomogeneous equation

        x_h represents the null space of A (the solution to the homogeneous equation)

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions