Change of Basis

Coordinates

Consider the vector v  =  (2,5,3) in R³.  In writing these coordinates we mean 

        v  =  2e₁ + 5e₂ + 3e₃ 

Where 

        e₁ =  (1,0,0)        e₂ =  (0,1,0)        e₃ =  (0,0,1)

are the standard basis vectors.  Sometimes we are interested in finding the coordinates with respect to another basis.  

Definition

Let S  =  {v₁, v₂, ... , v_n} be a basis for a vector space V and let v be a vector in V and let

        v  =  c₁v₁ + ... + c_nv_n  

Then the coordinates of v with respect to the basis S is given by

        [v]_S  =  (c₁, ... , c_n)

Example

Consider the basis 

        S  =  {(1,2), (4,7)} 

of R² and let 

        v  =  (5,8)

presented in the standard basis.  Find the coordinates of v in the basis S, that is find [v]_S.  

Solution

We set

     (5,8)  =  c₁(1,2) + c₂(4,7)   

or

         c₁ + 4c₂  =  5
        2c₁ + 7c₂  =  8

We get the matrix equation

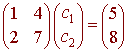
Notice that the matrix is just the matrix whose columns are the basis vectors of S.  The solution to this is

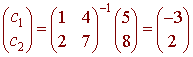
or

        c₁  =  -3        c₂  =  2

What we have seen here generalizes

Theorem

Let S  =  {v₁, v₂, ... , v_n} be a basis for a vector space V and let v be a vector in V.  Then

        [v]_S  =  A^-1v 

where A is the matrix whose column vectors are {v₁, v₂, ... , v_n} 

The proof involves going over the previous example and generalizing.

It is also interesting to run this process in reverse.  Let  S  =  {v₁, v₂, ... , v_n}be a basis for V and let [v]_S be given.  We ask how to present v in the standard basis.  This follows from the theorem.  Since

        [v]_S  =  A^-1v 

We have

        v  =  A[v]_S 

Example

Let 

        S  =  {(1,3,4), (2,-1,1), (1,0,2)} 

be a basis for R³ and let 

        [v]_S  =  (2,3,-1)

Find the coordinates with respect to the standard basis.  

Solution

We just find

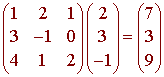
so that 

        v  =  (7,3,9)

Example

Let S  =  {(2,3), (1,4)} and T  =  {(0,2), (-1,5)} be two bases for R², and let 

        [v]_S  =  (-2,6)

Find [v]_T 

Solution

We can first find v in the standard basis.  We have

        v  =  A_S[v]_S 

where A_S is the matrix whose columns are the vectors in S.  Now convert to the T basis. 

        [v]_T  =  (A_T)^-1v   =  (A_T)^-1A_S[v]_S    

or 

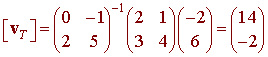
Example

Consider the vector v  =  2 + 3t - t² and let S  =  {t, t - 1, t² - 1}.  Find [v]_S.  

Solution

This problem looks a lot different from the previous ones, but looks can be deceiving.  We notice that 

        t       =      0(1) + 1(t) + 0(t²)
        t - 1  =      -1(1) + 1(t) + 0(t²)
        t² - 1  =      -1(1) + 0(t) + 1(t²)

We write that 

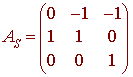
and use 

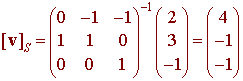
Transition Matrices

We have seen how to use the coordinates from one basis S into coordinates from another basis T.  We have

                [v]_T  =  (A_T)^-1A_S[v]_S  

The matrix given by

        P_{T <-- S}  =  (A_T)^-1A_S 

is called the transition matrix from the S basis to the T basis.  Note that the transition matrix from the T basis to the S basis is given by 

        P_{S <-- T}  =  (A_S)^-1A_T  =  P^-1_{T <-- S} 

Example

Find the transition matrix 

        P_{S <-- T}  

for the bases of M^2x2 given by

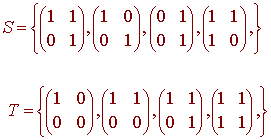
Then use this matrix to find [v]_S if 

        [v]_T  =  (1,3,-2,4)

Solution

First we denote the standard basis by 

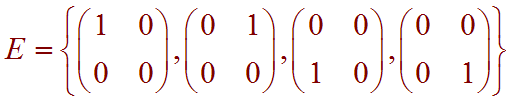
The A_S is just the matrix of column vectors where each column is read as you would read the matrices in S.  That is

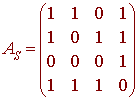
and similarly we have

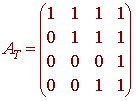
The transition matrix is 

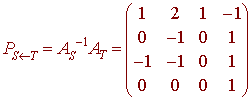
Now to find the coordinate in the S basis given T basis coordinates

        [v]_T  =  (1,3,-2,4)

we just multiply

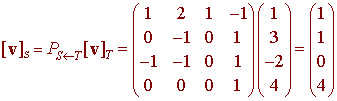
Remark:  The transition matrix will always be nonsingular because of the nonsingular equivalence and that S and T are linearly independent.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions