General Linear Transformations

Definition

We have seen that a linear transformation L from Rⁿ to R^m is a function with domain Rⁿ, range a subset of R^m satisfying

        1)  L(u + v)  =  L(u) + L(v)             2)  L(cu)  =  cL(u)

for any vectors u and v and scalar c.

We can use the analogous definition for a linear transformation of vector spaces.

Definition

Let V and W be vector spaces.  Then a linear transformation from V to W is a function with domain V and range a subset of W satisfying

        1)  L(u + v)  =  L(u) + L(v)             2)  L(cu)  =  cL(u)

for any vectors u and v  in V and scalar c.

Examples

Example

Let V be the vector space of (infinitely) differentiable functions and define D to be the function from V to V given by

       D(f(t))  =  f '(t)

Then D is a linear transformation since

        D(f(t) + g(t))  =  (f(t) + g(t))'  =  f '(t) + g'(t)  =  D(f(t)) + D(g(t))

and

        D(cf(t))  =  (cf(t))'  =  c f '(t)  =  cD(f(t))

Example

Let V be the space of continuous functions and define I to be the function from V to V given by

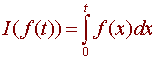
Then I is a linear transformation.  (Check this)

Example

Let V be M^2x2 and W be P₃ then define L to be the function from V to W with

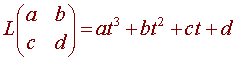
Then L is a linear transformation since

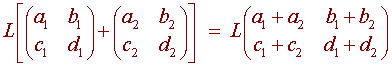
        =  (a₁ + a₂)t³ + (b₁ + b₂)t² + (c₁ + c₂)t + (d₁ + d₂)

        =  a₁t³ + b₁t² + c₁t + d₁ + a₂t³ + b₂t² + c₂t + d₂

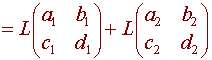
and

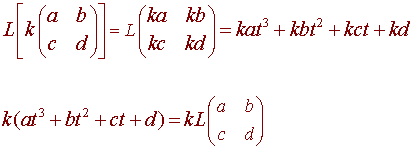
Example

Let V  =  P₂ and let W be the real numbers.  Show that the function L from V to W defined by

        L(at² + bt + c)  =  abc

is not a linear transformation.

Solution

 We can pick just about any example and show that either the first or second property does not hold.  For example, let

        v  =  2t² + 3t + 4        and        c  =  5

then

        L(cv)  =  L(10t² + 15t + 20)  =  (10)(15)(20)  =  3000

and

        cL(v)  =  5L(2t² + 3t + 4)  =  5(2)(3)(4)  =  120

since these are not equal, L is not a linear transformation.

Properties

When we looked at linear transformations from Rⁿ to R^m, we stated and proved several properties.  A close look at these proofs will show that they only used the properties of vector spaces and linearity.  We now state the properties.  For each of the theorems below, assume that L is a linear transformation from a vector space V to a vector space W, and u, v, v₁, v₂, ... ,v_n are vectors in V.

Theorem

1.  L(0)  =  0

2.  L(u - v)  =  L(u) - L(v)

3.  L(c₁v₁ + c₂v₂ + ... + c_nv_n)  =  c₁L(v₁) + c₂L(v₂) + ... + c_nL(v_n) 

We will prove statement 3 and leave the rest for you.  We prove the statement by induction.

For n  =  1, the statement is just property 2 of a linear transformation.

        L(c₁v₁)  =  c₁L(v₁)

Now assume that the statement is true for n  =  k.  Then

        L(c₁v₁ + c₂v₂ + ... + c_kv_k)  =  c₁L(v₁) + c₂L(v₂) + ... + c_kL(v_k) 

We have

        L(c₁v₁ + c₂v₂ + ... + c_kv_k + c_k+1v_k+1)  

        =  L((c₁v₁ + c₂v₂ + ... + c_kv_k) + c_k+1v_k+1) 

        =  L(c₁v₁ + c₂v₂ + ... + c_kv_k) + L(c_k+1v_k+1)  

        =   c₁L(v₁) + c₂L(v₂) + ... + c_kL(v_k) + c_k+1L(v_k+1)  

So by mathematical induction the theorem is true.

We have seen that general linear transformations behave the same as linear transformation from Rⁿ to R^m.  The next theorem solidifies this fact.

Theorem

Let S  =  {v₁, v₂, ... ,v_n} be a basis for V.  And let L be a linear transformation from V to a vector space W.  Then L is completely determined by the image of the basis S.

This means that if we know L(, L(v₂), ... ,L(v_n) then we know L(v) for any vector v.

Proof

If v is a vector in V, then since S is a basis, we can write

        v  =  c₁v₁ + c₂v₂ + ... + c_kv_k 

so that

        L(v)  =  L(c₁v₁ + c₂v₂ + ... + c_kv_k)  

        =  c₁L(v₁) + c₂L(v₂) + ... + c_kL(v_k) 

Example

Let L be the linear transformation from P₁ to M^2x2 such that 

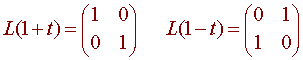
Find L(3 + t).

Solution

We need to find the coordinates of v  =  3 + t with respect to the basis S  =  {1 + t, 1 - t}.  We have 

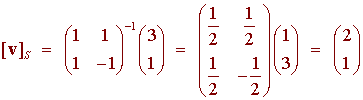
so that 

        v  =  2(1 + t) + 1(1 - t)

and

        L(v)  =  L(2(1 + t) + 1(1 - t))  =  2L(1 + t) + L(1 - t)

Back to the Vectors Home Page

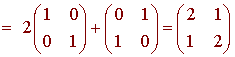
Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions